Find the value of (a+b+c)−d, if the following are in proportion.
12,48,c,36
To solve the problem, we need to find the value of (a+b+c)−d given that the numbers 12,48,c,36 are in proportion.
1. Understanding Proportions:
We know that if four numbers are in proportion, then the ratio of the first two numbers is equal to the ratio of the last two numbers. This can be expressed as:
\(
\frac{12}{48} = \frac{c}{36}
\)
2. Cross Multiplying:
To solve for c, we can cross-multiply:
\(
12 \times 36 = 48 \times c
\)
3. Calculating the Left Side:
Calculate \(12 \times 36\):
\(
12 \times 36 = 432
\)
4. Setting Up the Equation:
Now, we can set up the equation:
\(
432 = 48c
\)
5. Solving for c:
To find c, divide both sides by 48:
\(
c = \frac{432}{48}
\)
6. Calculating c:
Now, calculate \( \frac{432}{48} \):
\(
c = 9
\)
7. Finding a, b, c, and d:
Now we have:
- \(a = 12\)
- \(b = 48\)
- \(c = 9\)
- \(d = 36\)
8. Calculating (a + b + c):
Now, we can find \(a + b + c\):
\(
a + b + c = 12 + 48 + 9
\)
Calculate this:
\(
12 + 48 = 60
\)
\(
60 + 9 = 69
\)
9. Calculating (a + b + c) - d:
Now, subtract \(d\) from \(a + b + c\):
\(
(a + b + c) - d = 69 - 36
\)
Calculate this:
\(
69 - 36 = 33
\)
Final Answer:
The value of \((a + b + c) - d\) is 33.
We know that if four numbers are in proportion, then the ratio of the first two numbers is equal to the ratio of the last two numbers. This can be expressed as:
\(
\frac{12}{48} = \frac{c}{36}
\)
To solve for c, we can cross-multiply:
\(
12 \times 36 = 48 \times c
\)
Calculate \(12 \times 36\):
\(
12 \times 36 = 432
\)
Now, we can set up the equation:
\(
432 = 48c
\)
To find c, divide both sides by 48:
\(
c = \frac{432}{48}
\)
Now, calculate \( \frac{432}{48} \):
\(
c = 9
\)
Now we have:
- \(a = 12\)
- \(b = 48\)
- \(c = 9\)
- \(d = 36\)
Now, we can find \(a + b + c\):
\(
a + b + c = 12 + 48 + 9
\)
Calculate this:
\(
12 + 48 = 60
\)
\(
60 + 9 = 69
\)
Now, subtract \(d\) from \(a + b + c\):
\(
(a + b + c) - d = 69 - 36
\)
Calculate this:
\(
69 - 36 = 33
\)
The value of \((a + b + c) - d\) is 33.
Topper's Solved these Questions
- RATIO AND PROPORTIONBOOK - MTG IIT JEE FOUNDATIONCHAPTER - RATIO AND PROPORTIONEXERCISE - OLYMPAID/HOTS CORNER
15 Videos
- RATIO AND PROPORTIONBOOK - MTG IIT JEE FOUNDATIONCHAPTER - RATIO AND PROPORTIONEXERCISE - EXERCISE (SUBJECTIVE PROBLEMS)(LONG ANSWER TYPE)
5 Videos
- PREP TEST -1BOOK - MTG IIT JEE FOUNDATIONCHAPTER - PREP TEST -1EXERCISE - SECTION-B
35 Videos
- SYMMETRYBOOK - MTG IIT JEE FOUNDATIONCHAPTER - SYMMETRYEXERCISE - Olympiad/HOTS Corner
13 Videos
Similar Questions
Find the value of (a+b+c)−d, if the following are in proportion.
72,144,24,d
View SolutionFind the value of (a+b+c)−d, if the following are in proportion.
a,30,40,60
View SolutionFind the value of (a+b+c)−d, if the following are in proportion.
10,b,24,60
View SolutionDetermine if the following are in proportion.
24, 28, 36, 48
View SolutionDetermine if the following are in proportion :
24: 28, 36:48
View SolutionFind the value of ∣∣∣dbca∣∣∣
View SolutionFind the value of ∣∣∣dbca∣∣∣ is
View SolutionFind the values of A,B,C,D,E,F,G in the following
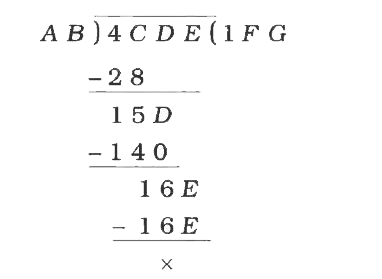
View SolutionState True or False:
If b : a = c : d, then a, b, c, d are in proportion.
View SolutionDetermine if the following are in proportion.
(a) 15, 45, 40, 120
(b) 33, 121, 9,96
(c) 24, 28, 36, 48
(d) 32, 48, 70, 210
(e) 4, 6, 8, 12
(f) 33, 44, 75, 100
View Solution
