Find the value of: ω768
To find the value of ω768, we need to use the property that ω3=1. This means that ω is a cube root of unity.
1. Understand the property of ω:
Since ω3=1, any power of ω can be simplified by reducing the exponent modulo 3. This is because ωn will repeat every 3 powers.
2. Calculate 768mod3:
To find 768mod3, we divide 768 by 3 and find the remainder.
768÷3=256(exact division, remainder 0)
Therefore, 768mod3=0.
3. Simplify ω768:
Since 768mod3=0, we can write:
ω768=ω3⋅256=(ω3)256
4. Use the property of ω3:
We know ω3=1, so:
(ω3)256=1256=1
5. Conclusion:
Therefore, the value of ω768 is:
1
Since ω3=1, any power of ω can be simplified by reducing the exponent modulo 3. This is because ωn will repeat every 3 powers.
To find 768mod3, we divide 768 by 3 and find the remainder.
768÷3=256(exact division, remainder 0)
Therefore, 768mod3=0.
Since 768mod3=0, we can write:
ω768=ω3⋅256=(ω3)256
We know ω3=1, so:
(ω3)256=1256=1
Therefore, the value of ω768 is:
1
Similar Questions
Find the value of: ω−364
View SolutionFind the value of: ω−30
View SolutionFind the value of: ω−105
View SolutionFind the value of: ω−105
View SolutionFind the value of(i)ω21(ii)ω18
View SolutionReduce the equation √3x+y−8=0 into normal form. Find the values of p and ω.
View SolutionA vertical U-tube is spinned about the vertical axis passing through the left hand limb, with an angular speed ω such that the liquid columns in the limbs have heights h and 3h, as shown in the figure. Find the value of to ω.
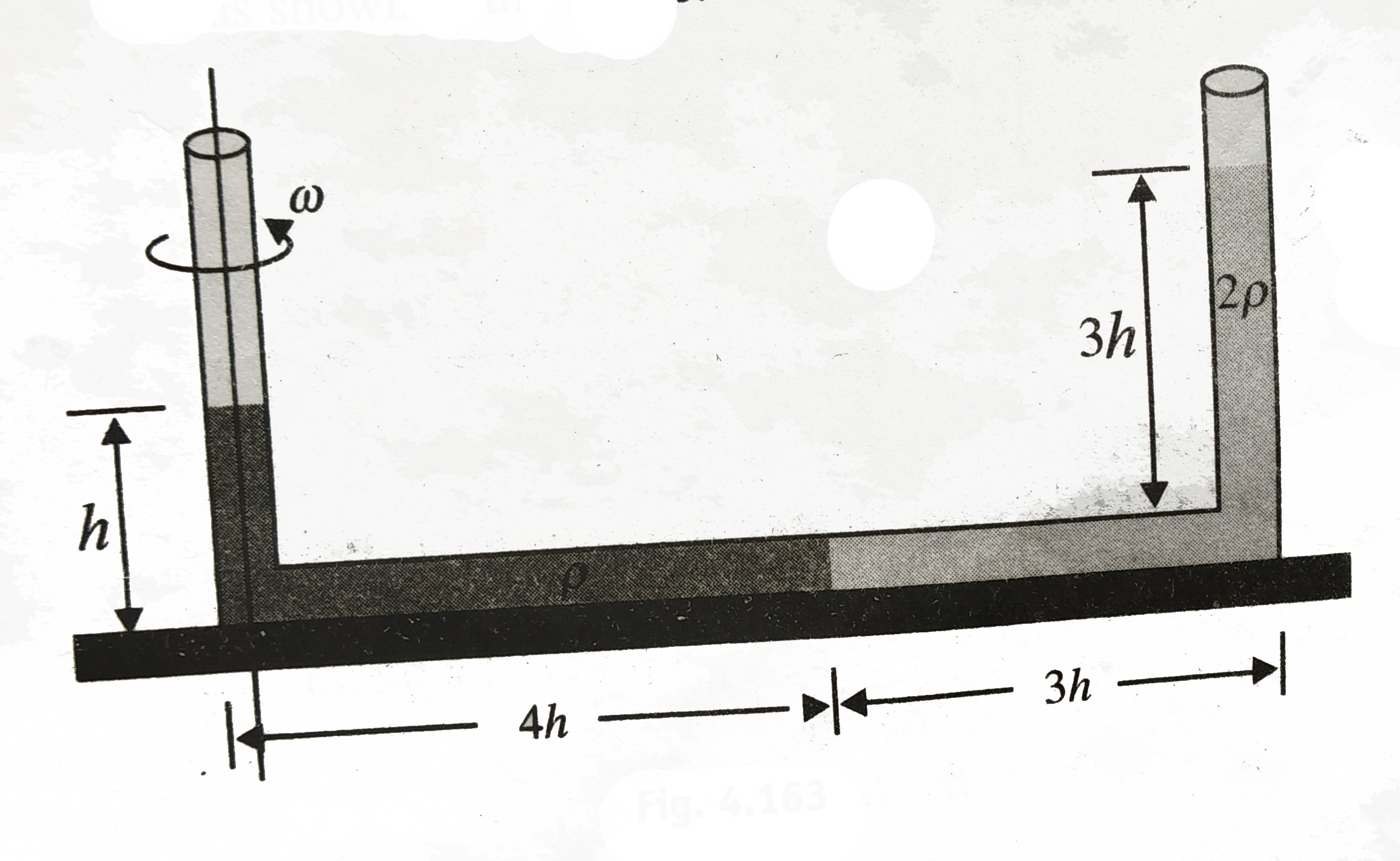
View SolutionIf ω is a cube root of unity then find the value of sin((ω10+ω23)π−π4)
View SolutionIf ω is a cube root of unity then find the value of sin((ω10+ω23)π−π4)
View SolutionIf ω is a complex cube roots of unity, then find the value of the (1+ω)(1+ω2)(1+ω4)(1+ω8)… to 2n factors.
View Solution
