Find the value of p for the following distribution whose mean is 12.58. p and
To find the value of p for the given distribution with a mean of 12.58, we will follow these steps:
Step 1: Set up the data
We have the following values for x and f:
xf52851081222p7204252
Step 2: Calculate f⋅x
We will calculate the product of each x value and its corresponding frequency f:
xff⋅x525⋅2=10858⋅5=4010810⋅8=80122212⋅22=264p77p20420⋅4=8025225⋅2=50
Step 3: Sum f⋅x and f
Now we will find the summation of f⋅x and f:
Sum of f⋅x=10+40+80+264+7p+80+50=524+7p
Sum of f=2+5+8+22+7+4+2=50
Step 4: Use the mean formula
The mean ¯x is given by the formula:
¯x=∑(f⋅x)∑f
Substituting the known values:
12.58=524+7p50
Step 5: Solve for p
Now, we will solve for p:
1. Multiply both sides by 50:
12.58×50=524+7p
Calculating 12.58×50:
629=524+7p
2. Rearranging gives:
7p=629−524
Calculating 629−524:
7p=105
3. Finally, divide by 7:
p=1057=15
Conclusion
The value of p is 15.
---
We have the following values for x and f:
We will calculate the product of each x value and its corresponding frequency f:
Now we will find the summation of f⋅x and f:
The mean ¯x is given by the formula:
Now, we will solve for p:
The value of p is 15.
Topper's Solved these Questions
Similar Questions
Find the value of p for the following distribution whose mean is 16.6. x:8,12,15,p,20,25,30 and f:12,16,20,24,16,8,4
View SolutionFind the missing value of for the following distribution whose mean is 12.58 5 8 10 12 20 25 2 5 8 22 7 4 2
View SolutionFind the value of p for the following distribution whose mean is 16.6 8 12 15 20 25 30 12 16 20 24 16 8 4
View SolutionFind the value of p, if mean of the following distribution is 7.5.
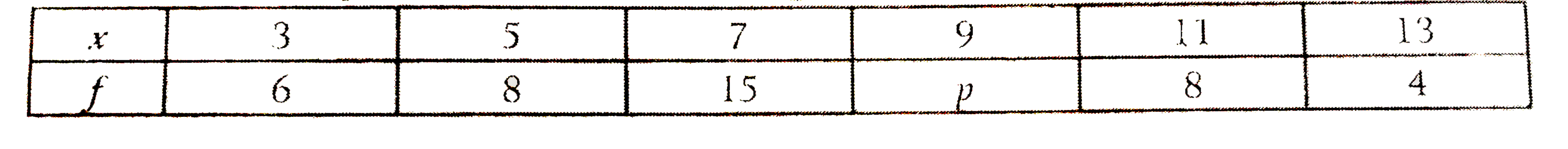 View Solution
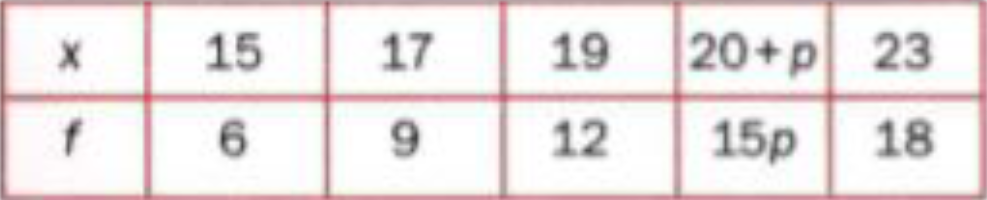
View SolutionFind the value of p, if the mean of following distribution is 20.
 View Solution
View SolutionFind the value of P if the mean of the following distribution is 7.5
 View Solution
View SolutionFind the value of p , if the mean of the following distribution is 20. x:15,17,19,20+p,23 and f : 2, 3, 4, 5p, 6
View SolutionFind the mean of the following distribution: 4 6 9 10 15 5 10 10 7 8
View SolutionFind the missing frequency for the following distribution whose mean is 7.68
x:3 5 7 9 11 13
y:6 8 15 p 8 4View SolutionFind the value of p, if the mean of the following distribution is 7.5. x: 3 5 7 9 11 13 f: 6 8 15 p 8 4
View Solution

