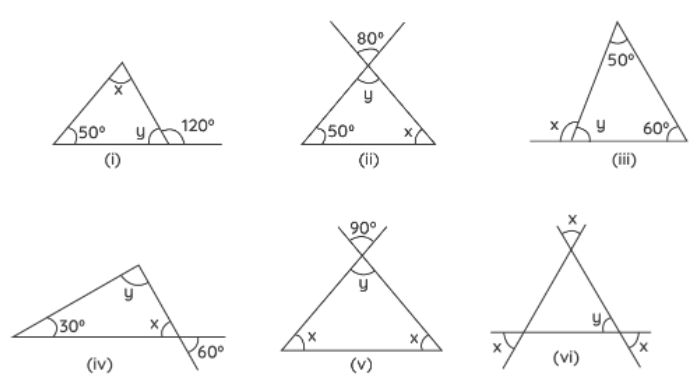
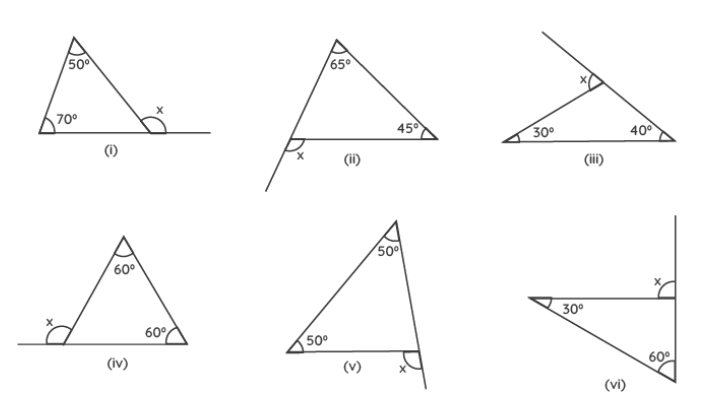
Find the value of the unknown x in the following diagrams:
To find the value of the unknown x in the given triangles, we will use the property that the sum of the interior angles of a triangle is always 180∘.
1. First Triangle:
- Given angles: x, 50∘, and 60∘.
- Set up the equation based on the sum of angles:
x+50+60=180
- Combine the known angles:
x+110=180
- Solve for x:
x=180−110
x=70∘
2. Second Triangle:
- Given angles: x, 30∘, and a right angle (90∘).
- Set up the equation:
x+30+90=180
- Combine the known angles:
x+120=180
- Solve for x:
x=180−120
x=60∘
3. Third Triangle:
- Given angles: x, 30∘, and 110∘.
- Set up the equation:
x+30+110=180
- Combine the known angles:
x+140=180
- Solve for x:
x=180−140
x=40∘
4. Fourth Triangle:
- Given angles: 2x and 50∘.
- Set up the equation:
2x+50=180
- Solve for 2x:
2x=180−50
2x=130
- Divide by 2 to find x:
x=1302
x=65∘
5. Fifth Triangle:
- Given angles: x, 2x, and 90∘.
- Set up the equation:
x+2x+90=180
- Combine the terms:
3x+90=180
- Solve for 3x:
3x=180−90
3x=90
- Divide by 3 to find x:
x=903
x=30∘
Summary of Values:
- For the first triangle, x=70∘
- For the second triangle, x=60∘
- For the third triangle, x=40∘
- For the fourth triangle, x=65∘
- For the fifth triangle, x=30∘
- Given angles: x, 50∘, and 60∘.
- Set up the equation based on the sum of angles:
x+50+60=180
- Combine the known angles:
x+110=180
- Solve for x:
x=180−110
x=70∘
- Given angles: x, 30∘, and a right angle (90∘).
- Set up the equation:
x+30+90=180
- Combine the known angles:
x+120=180
- Solve for x:
x=180−120
x=60∘
- Given angles: x, 30∘, and 110∘.
- Set up the equation:
x+30+110=180
- Combine the known angles:
x+140=180
- Solve for x:
x=180−140
x=40∘
- Given angles: 2x and 50∘.
- Set up the equation:
2x+50=180
- Solve for 2x:
2x=180−50
2x=130
- Divide by 2 to find x:
x=1302
x=65∘
- Given angles: x, 2x, and 90∘.
- Set up the equation:
x+2x+90=180
- Combine the terms:
3x+90=180
- Solve for 3x:
3x=180−90
3x=90
- Divide by 3 to find x:
x=903
x=30∘
- For the first triangle, x=70∘
- For the second triangle, x=60∘
- For the third triangle, x=40∘
- For the fourth triangle, x=65∘
- For the fifth triangle, x=30∘
Topper's Solved these Questions
- THE TRIANGLE AND ITS PROPERTIESBOOK - NCERTCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - SOLVED EXAMPLES
6 Videos
- THE TRIANGLE AND ITS PROPERTIESBOOK - NCERTCHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 6.4
6 Videos
- SYMMETRYBOOK - NCERTCHAPTER - SYMMETRYEXERCISE - EXERCISE 14.1
9 Videos
Similar Questions
Knowledge Check
The value of stopping potential in the following diagram
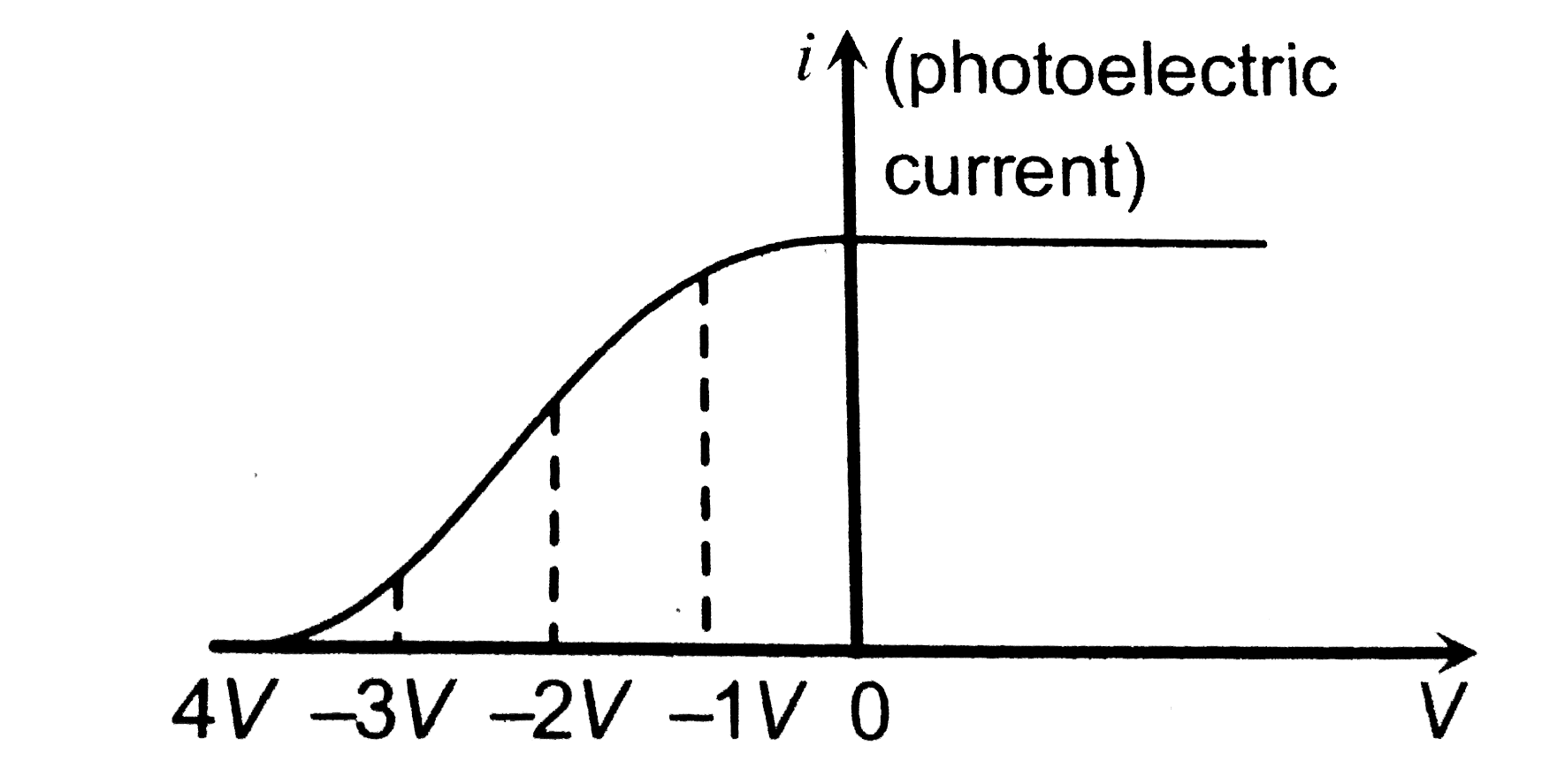 A−4VB−3VC−2VD−1V
A−4VB−3VC−2VD−1V
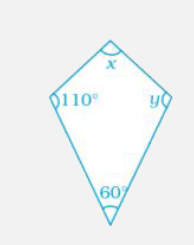
Find the values of x and y in the following kite.
View SolutionFind the value of the unknown resistance X, in the following circuit if no current flows through the arm AO from the battery of 6V and negligible internal resistance. Also find the Current flowing from the battery.
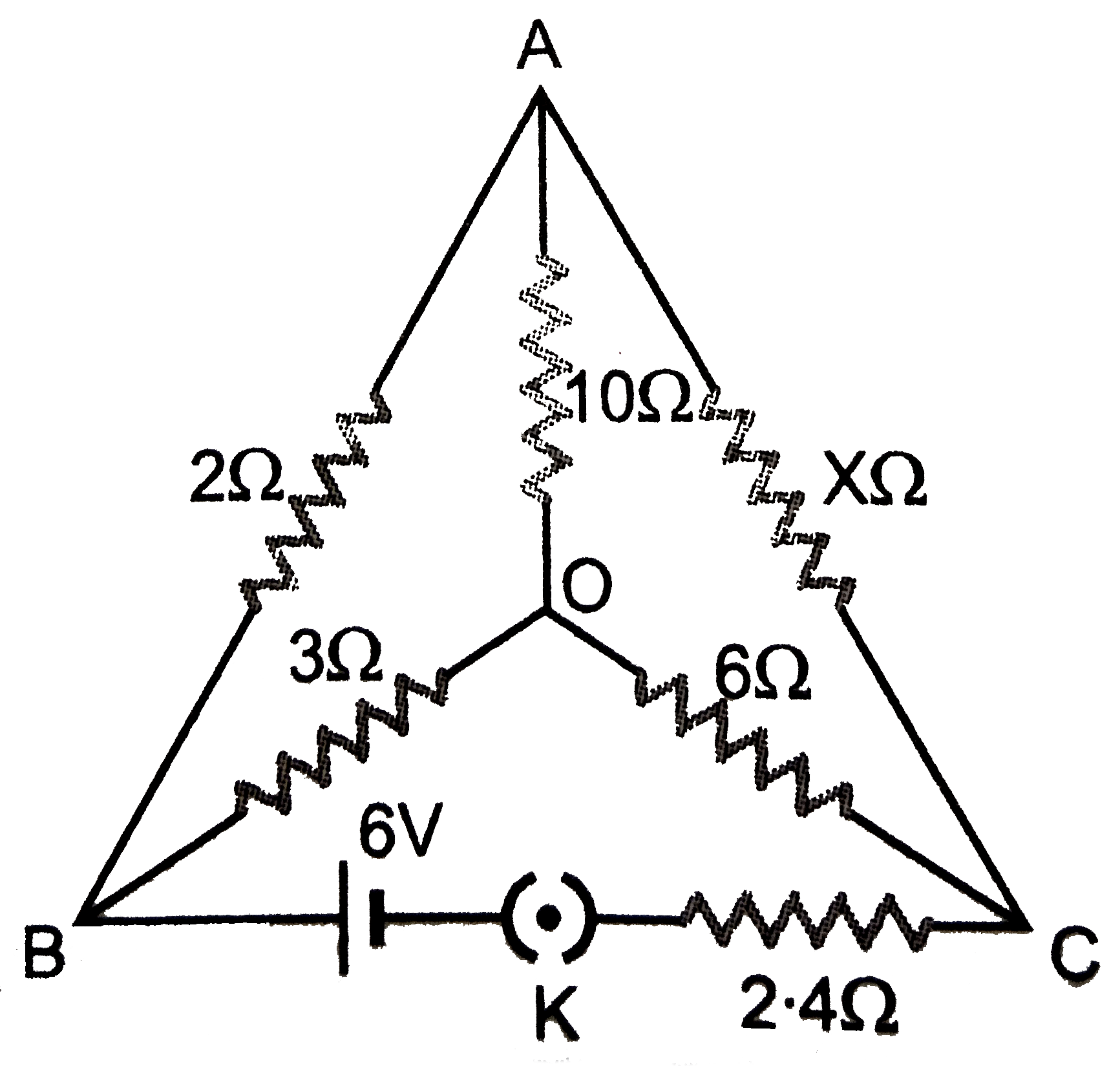
View SolutionFind the values of x and y in the following rectangle.

View SolutionFind the values of x and y in the following parallelogram.

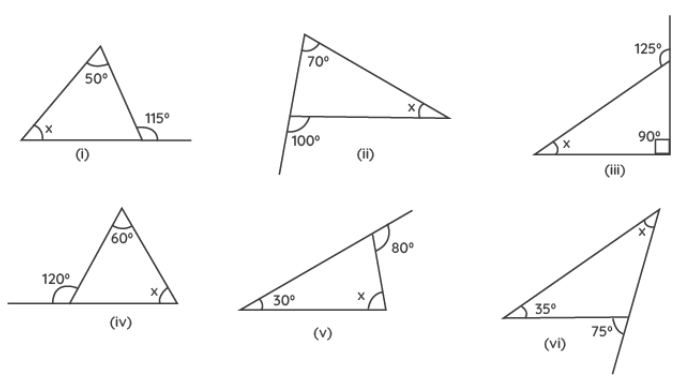
View SolutionFind the value of the unknown exterior angle x in the following diagrams:
View SolutionFind the value of the unknown interior angle x in the following figures:
View SolutionFind the unknown angle in the following :
View Solution