Find the value of x for which f(x)=√sinx−cosx is defined, x∈[0,2π).Solution in Bengali
f(x)=√sinx−cosx is defined if sinx≥cosx.
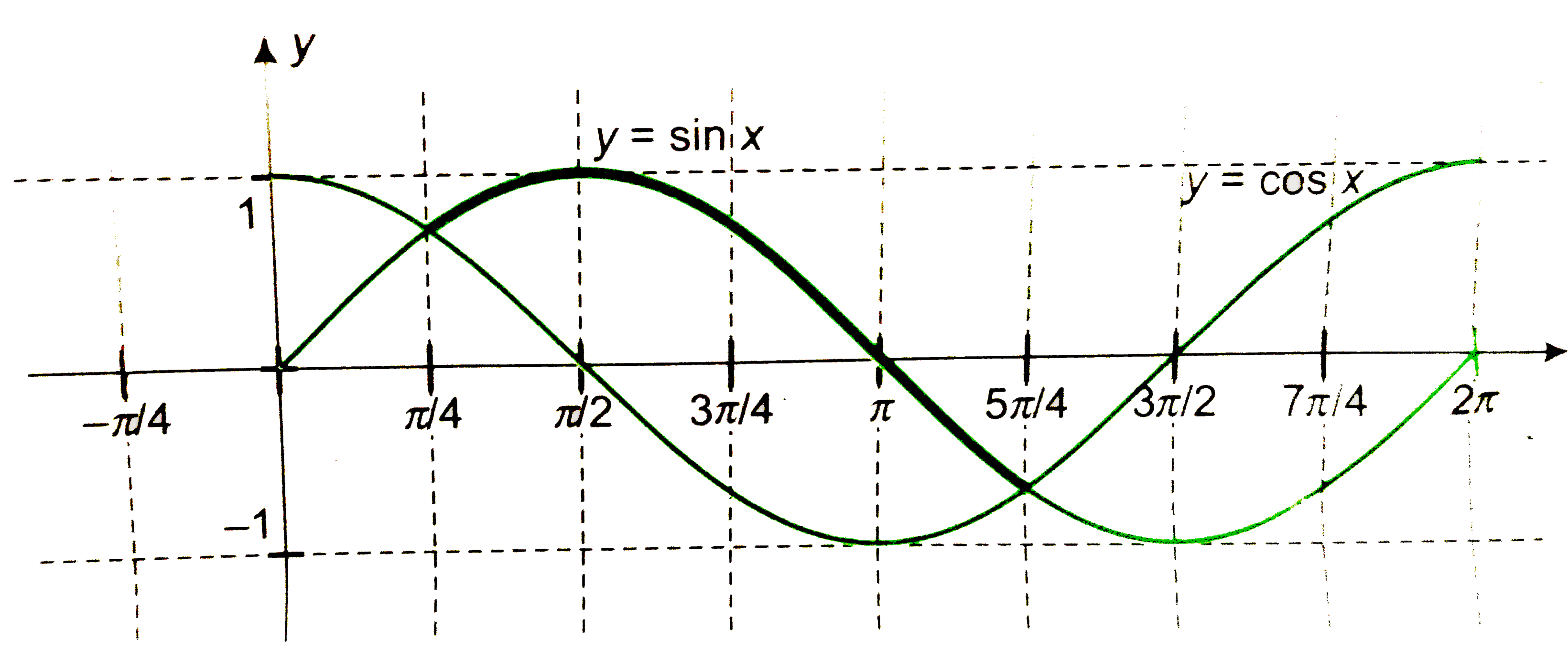
From the graph, sinx≥cosx,forx∈[π4,5π4].
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - example
10 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Concept Application Exercises 2.1
8 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)
4 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Archives (Numerical Value Type)
2 Videos
Similar Questions
If 2cosx+sinx=1, then find the valie of 7x+6sinx.
View SolutionTwo sides of a parallelogram are 12 cm and 8 cm. If one of the interior angles is 135∘, then find area of the parallelogram.
View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
View SolutionThe maximum value of the expression 1sin2θ+3sinθcosθ+5cos2θ is………
View SolutionIf [sinx]+[√2cosx]=−3,x∈[0,2π]([.]−GIF),thenx∈
View SolutionIf a function is defined as f(x)=√logh(x)g(x), where g(x)=|sinx|+sinx,h(x)=sinx+cosx,0≤x≤π. Then find th domain of f(x).
View SolutionFind all the points of local maxima and minima of the function f given by f(x)=sinx−cosx,x∈[0,2π]
View SolutionIf f(x) =∣∣ ∣∣sinxcosxsinxcosx−sinxcosxx11∣∣ ∣∣ find the value of 2(f'(o))+{f'(1)}2
View Solutionयदि f(x)=sinxcosx+cosxsinx+logax, तो f'(x) का मान ज्ञात कीजिए |
View SolutionFor what values of x is the function f(x)=sinxcosx−sinx not defined ?
View SolutionFind the value of x for which f(x)=√sinx−cosx is defined, x∈[0,2π).
View SolutionSolve |sinx+cosx|=|sinx|+|cosx|,x∈[0,2π].
View SolutionLet f(x)=sinx−cosx be defined on [0,2π]. Determine the intervals in which f(x) is strictly decreasing and strictly increasing.
View SolutionIf f(x)=∣∣ ∣∣sinxcosxsinxcosx−sinxcosxx11∣∣ ∣∣ find the value of 2[f'(0)]+[f'(1)]2
View SolutionFind all the points of local maxima and minima of the function f given by f(x)=sinx−cosx,x∈[0,2π]
View SolutionConsider the functions f(x)=sinx and g(x)=cosx in the interval [0,2pi] Find the x coordinates of the meeting points of the functions.
View Solution
