Find the values of a and b from the adjoining figure.
To find the values of a and b from the given figure, we will follow these steps:
Step 1: Identify the angles on a straight line
Since OT stands on the straight line PQ, we know that the sum of the angles on a straight line is 180∘. Therefore, we can write the equation:
∠POT+∠TOQ=180∘
Step 2: Write the angles in terms of a and b
From the figure, we have:
∠POT=3a+22∘
∠TOQ=47∘
Substituting these into the equation gives us:
(3a+22∘)+47∘=180∘
Step 3: Simplify the equation
Combine the constants:
3a+69∘=180∘
Step 4: Solve for a
Subtract 69∘ from both sides:
3a=180∘−69∘
3a=111∘
Now, divide by 3:
a=111∘3=37∘
Step 5: Use the angles in another equation
Now we will consider the angles ∠POR, ∠ROS, and ∠SOQ. We know that their sum is also 180∘:
∠POR+∠ROS+∠SOQ=180∘
Given that:
∠POR=90∘,∠ROS=a,∠SOQ=b+18∘
Substituting the known values gives us:
90∘+37∘+(b+18∘)=180∘
Step 6: Simplify and solve for b
Combine the constants:
145∘+b=180∘
Now, subtract 145∘ from both sides:
b=180∘−145∘
b=35∘
Final Values
Thus, the values of a and b are:
a=37∘,b=35∘
Since OT stands on the straight line PQ, we know that the sum of the angles on a straight line is 180∘. Therefore, we can write the equation:
From the figure, we have:
∠TOQ=47∘
Combine the constants:
Subtract 69∘ from both sides:
3a=111∘
Now we will consider the angles ∠POR, ∠ROS, and ∠SOQ. We know that their sum is also 180∘:
Combine the constants:
b=35∘
Thus, the values of a and b are:
Topper's Solved these Questions
- LINES AND ANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Problems From NCERT/exemplar
6 Videos
- LINES AND ANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6 A
19 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Revision Exercise
12 Videos
- NUMBER SYSTEMBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - NUMBER SYSTEMEXERCISE - Revision Exercise (short Answer Questions)
10 Videos
Similar Questions
Find the measure of ∠x in the adjoining figure.

View SolutionFind the value of x form the adjoining diagram.

View SolutionFind the values of x and y from adjoining parallelogram.
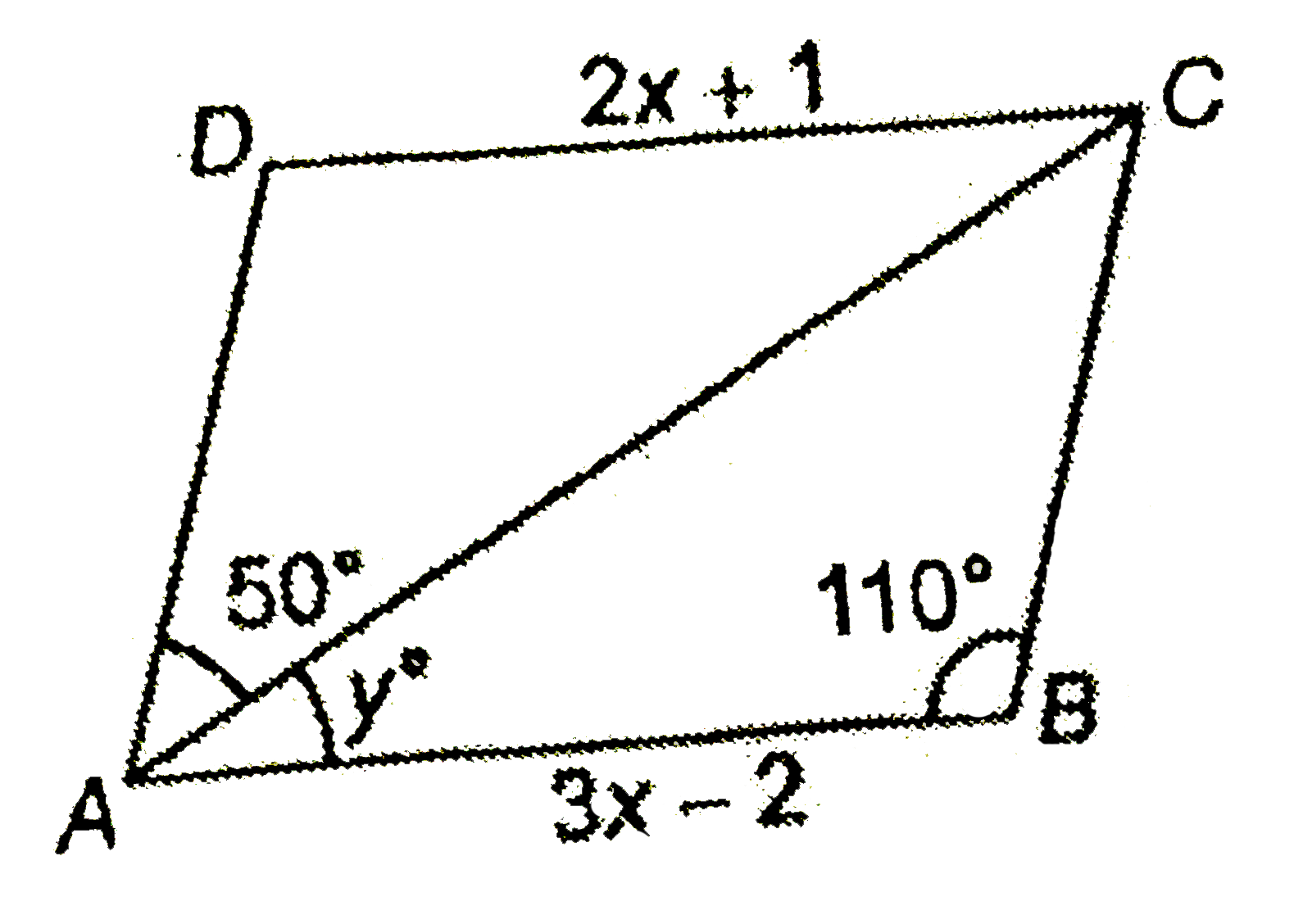
View SolutionCalculate the value of x in the adjoining figure.

View Solution(i) In the adjoining figure, find the value of ∠CBE.

(ii) In the adjoining figure, two lines PAB and PDC cut a circle at points A,B,C and D. if ∠PAD=60∘,then find the value of ∠BCD.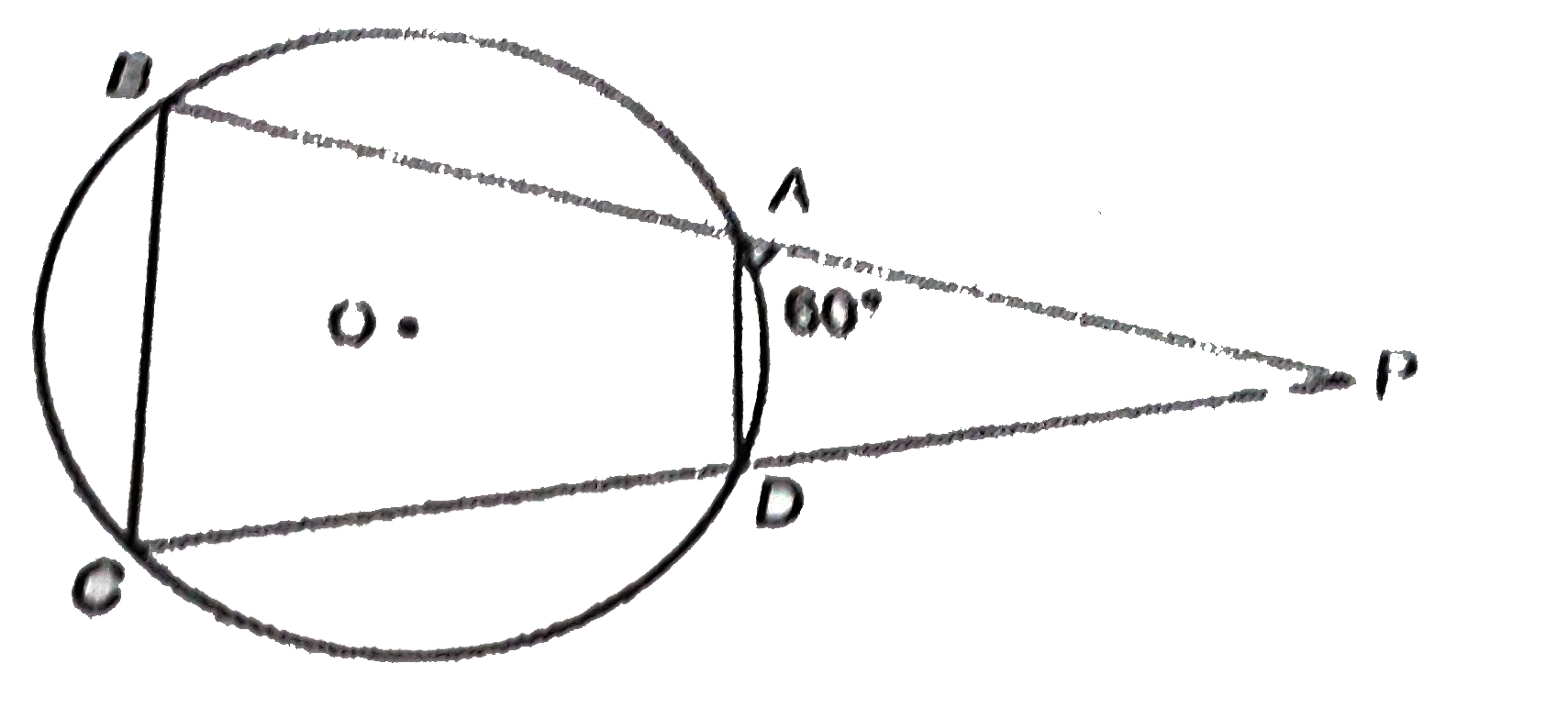
View SolutionIn the adjoining figure find ∠x
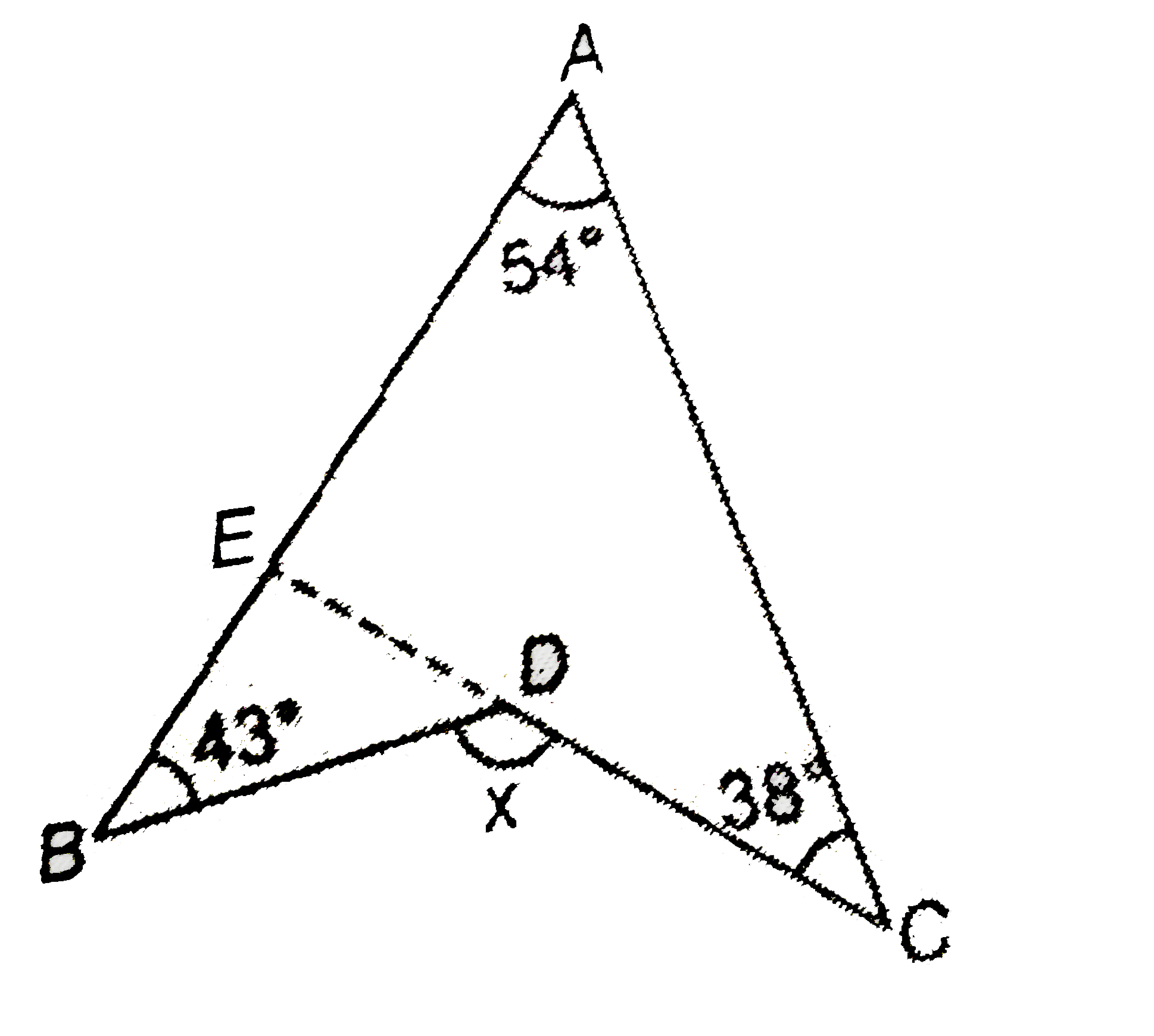
View SolutionIn the adjoining figure find ∠x
View Solution(i) In the adjoining figure, O is the centre of the circle. If ∠OBC=35∘, then find the value of ∠BAC.

(ii) In the adjoining figure, O is the centre of the circle. If ∠OBC=40∘, then find the value of ∠BAC.

View SolutionFind the value of CD in terms of x, in the adjoining figure, where O is the centre of semicircle.
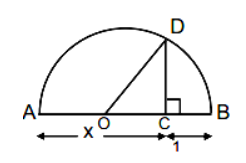
View SolutionFind the area of the trapezium given in adjoining figure.

View Solution
