Find the values of β so that the point (0,β) lies on or inside the triangle havind the sides 3x+y+2=0,2x−3y+5=0andx+4y−14=0.
[53,∞)
(−∞,72]
[53,72]
none of these
The correct Answer is:C
Let ABC be the given triangle. The coordinates of the vertices of the triangle ABC are marked in fig. 12 . The point P(0,β) will lie inside or on the triangle ABC, if the following three conditions hold simultaneously.
(i) A and P lie on the same side of BC,
(ii) B and P lie on the same side of AC,
(iii) C and P lie on the same side of AB.
Now, A and P will lie on the same side of BC, if
(3×2+3+2)(3×0+β+2)>0
⇒11(β+2)≥o⇒β+2≥0⇒β≥−2 (i)
B and P will lie on the same side of AC, if
(−2×2−3×4+5)(2×0−3β+5)≥0
⇒−11(−2β+5)≥0⇒3β−5≤0⇒β≥53 ...(ii)
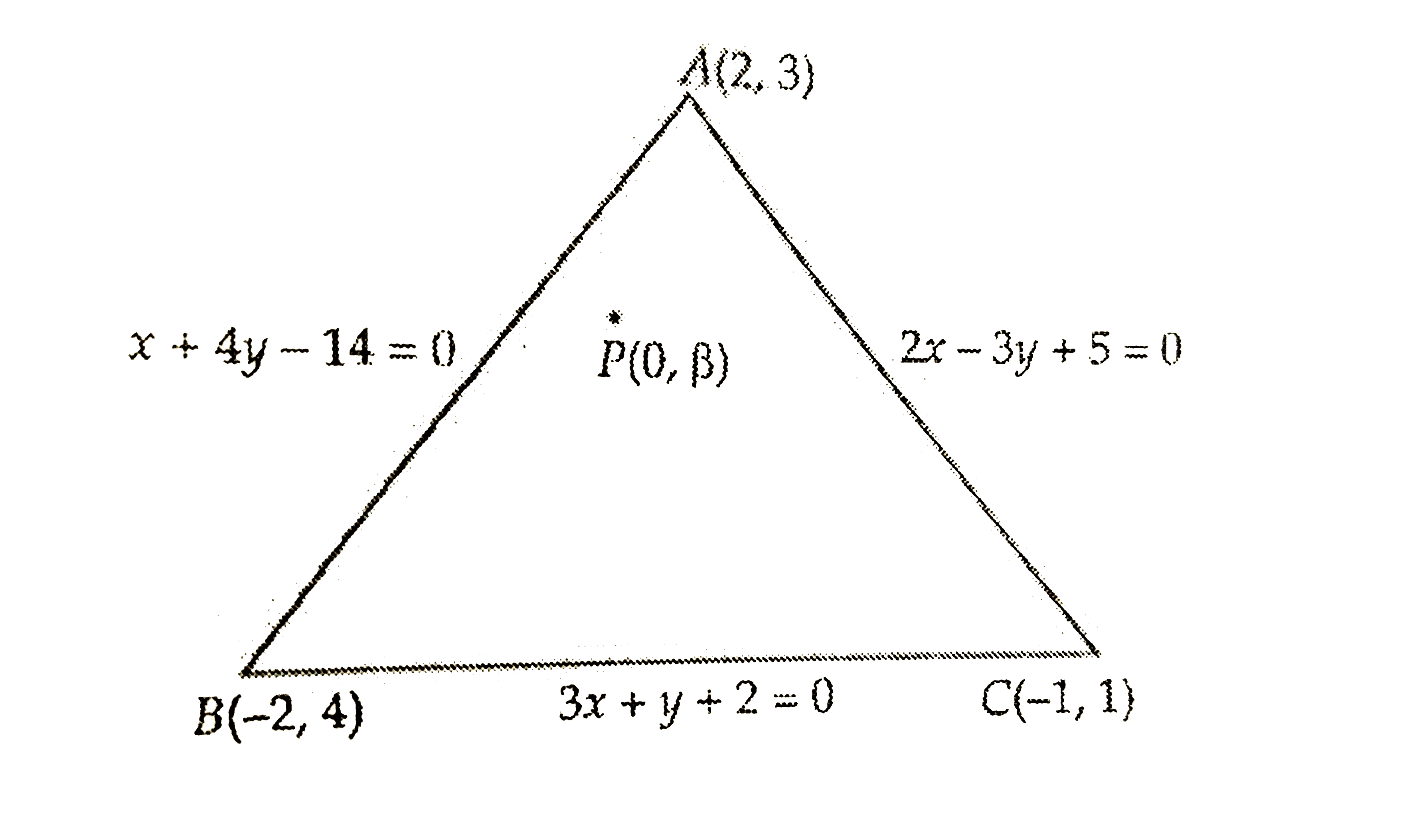
(−1+1×4−14)(0+4β−14)≥0
⇒−22(2β−7)≥0⇒2β−7≤0⇒β≤72 ...(iii)
From (i), (ii) and (iii), we obtain that
53≤β≤72i.e.β∈[53,72]
Topper's Solved these Questions
Similar Questions
Knowledge Check
Point (0,β) lies on or inside the triangle fromed by the lines y=0,x+y=8 and 3x−4y+12=0. Then β can be :
A2B4C8D12
Find the values of the parameter a so that the point (a, 2) is an interior point of the triangle formed by the lines x+y-4=0, 3x-7y-8=0and 4x-y-31 = 0.
View SolutionFind the value of c so that the point (3,c) lies on the line represented by 2x-3y+5=0.
View SolutionThe exhaustive range of a for which the point (a,0) lies inside the triangle formed by the lines y+3x+2=0, 3y−2x−5=0 and 4y+x−14=0 is
View SolutionThe range of value of α such that (0,α) lies on or inside the triangle formed by the lines y + 3x + 2 = 0, 3y - 2x - 5 = 0, 4y + x - 14 =0 is
View SolutionTrue set of real values of a such that the point M(a,sin a) lies inside the triangle formed by x-2y+ 2 = 0, x+y=0 and x-y-π=0 is :
View SolutionStatement 1: The value of α for which the point (α,α2) lies inside the triangle formed by the lines x=0,x+y=2 and 3y=x is (0,1). Statement 2: The parabola y=x2 meets the linex+y=2 at(0,1).
View SolutionThe number of integral values of 'a for which the point (a,a2) lies completely inside the triangle x=0,y=0,2y+x=3 is
View Solution
