Find the variance and standard deviation of the random variable X whose probability distribution is given below :
To find the variance and standard deviation of the random variable X with the given probability distribution, we will follow these steps:
Step 1: Calculate the Mean (Expected Value) E(X)
The mean E(X) is calculated using the formula:
E(X)=∑(xi⋅P(X=xi))
Given the probability distribution:
- x=0, P(X=0)=18
- x=1, P(X=1)=38
- x=2, P(X=2)=38
- x=3, P(X=3)=18
Now, substituting the values:
E(X)=0⋅18+1⋅38+2⋅38+3⋅18
Calculating each term:
E(X)=0+38+68+38=128=32
Step 2: Calculate E(X2)
Next, we calculate E(X2) using the formula:
E(X2)=∑(x2i⋅P(X=xi))
Substituting the values:
E(X2)=02⋅18+12⋅38+22⋅38+32⋅18
Calculating each term:
E(X2)=0+38+128+98=248=3
Step 3: Calculate Variance Var(X)
The variance is calculated using the formula:
Var(X)=E(X2)−(E(X))2
Substituting the values:
Var(X)=3−(32)2
Calculating (32)2:
(32)2=94
Now substituting back into the variance formula:
Var(X)=3−94
To perform the subtraction, convert 3 into a fraction:
3=124
Now we can subtract:
Var(X)=124−94=34
Step 4: Calculate Standard Deviation SD(X)
The standard deviation is the square root of the variance:
SD(X)=√Var(X)=√34=√32
Final Result
- Variance Var(X)=34
- Standard Deviation SD(X)=√32
---
- x=1, P(X=1)=38
- x=2, P(X=2)=38
- x=3, P(X=3)=18
- Standard Deviation SD(X)=√32
Topper's Solved these Questions
- MARCH 2018BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2018EXERCISE - SECTION - II
20 Videos
- MARCH 2017BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2017EXERCISE - SECTION-II
20 Videos
- MARCH 2019BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2019EXERCISE - SECTION-D
13 Videos
Similar Questions
Knowledge Check
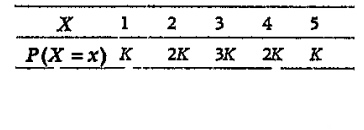
A random variable X has the probability distribution given below
Its variance isA163B43C53D103If X is a random -variable with distribution given below :
x:0123p(x):k3k3kk
The value of k and its variance areA1/8,22/27B1/8,23/27C1/8,24/27D1/8,3/4If the standard deviation of the random variable X is √3pq and mean is 3p then E(x2)= . . .
A3pq+3q2B3p(1+2p)C3pq+3p2D3p(1+2q)
A random variable X has the following probability distribution: [X=x0123P(X=x)181214k]
View SolutionFind expected value of the random Variable X whose probability mass function is X=x,1,2,3<br>P(X=x)15,25,25
View SolutionThe variance of the random variable X having the following distribution is X=x:−2−1012P(X=x):1616131616
View SolutionFind the mean and standard deviation of the following probability distribution: xi:−5 −4 1 2 pi:14 18 12 18
View SolutionSelect and write the correct answer from the given alternatives in each of the following :
A random variable X has the following probability distribution :
X=x−2−10123P(x)0.10.10.20.20.30.1
Then E(x) = ………
View Solution


