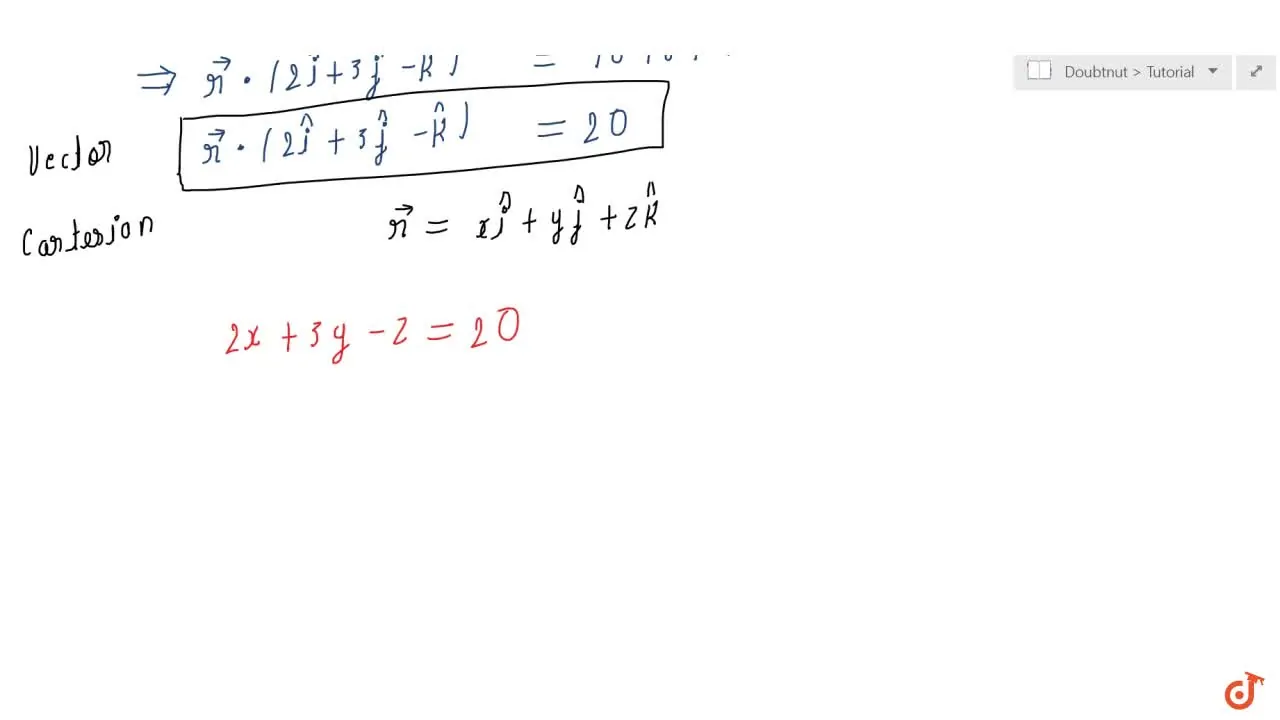Find the vector and cartesian equations of the plane which passes through the point (5,2,4)and perpendicular to the line with direction ratios (2,3,1).
Let A(5,2,4) is the point passing through given plane.
In vector form,
→A=5ˆi+2ˆj+4ˆk
Let →r is another vector on that plane, then, line joining →r and →a will be,
→r−→A
We are given another line with direction cosines (2,3,1) that is perpendicular to the first line.
So, dot product of these two lines will be 0.
∴(→r−(5ˆi+2ˆj+4ˆk)).(2ˆi+3ˆj+ˆk)=0
⇒→r.(2ˆi+3ˆj+ˆk)−10−6−4=0
⇒→r.(2ˆi+3ˆj+ˆk)=20
We can take, →r=aˆi+bˆj+cˆk
Then, our equation becomes,
2a+3b+c=20, which is required vector equation.
Cartesian equation will be,
2x+3y+z=20
Similar Questions
Find the vector and the Cartesian equation of the plane which pases through the point (5,2,-4) and perpendicular to the line with direction ratios (2,3,-1).
View SolutionThe Cartesian equations of the plane which passes through the point (5,2,−4) and perpendicular to the line with direction ration 2,3,−1 is
View SolutionFind the vector and cartesian equation of the plane :
(i) that passes through the point (5,2,-4) and perpendicular to the line with direction-ratios <2,3,−1>
(ii) that passes through the point (1,0, -2) and the normal to the plane is ˆi+ˆj−ˆk
(iii) that passes through the point (1,4,6) and the normal vector to the plane is ˆi−2ˆj+ˆk.View SolutionFind the vector and the Cartesian equations of the plane passing through the point (1,2,3) and perpendicular to the line with direction ratio 2,3,−4.
View SolutionFind the vector and Cartesian equations of the plane passing throgh the point (2,-1,1) and perpendicular to the line having direction ratios 4,2,-3.
View SolutionFind the vector equation of tha plane which passes through the point (3, 2, -3) and perpendicular
to a line with direction ratios (1, 2, -1).View SolutionFind the vector and cartesian equation of a plane which passes through the point (2,−1,3) and perpendicular to a line whose d.r.'s are 1,−3,5.
View SolutionFind the vector and cartesian equation of a line passes through the points (1,3,2) and origin.
View SolutionFind the vector and the cartesian equations of the lines that passes through the origin and (5,−2,3).
View SolutionFind the vector and Cartesian equations of the line passing through the points A(3,4-6) and B(5,-2,7) .
View Solution