Find the volume and whole surface of frustum of a square pyramid , thje sides of whose base and top are 24 cm and 16 cm respectively and each of the edges of the frustum is 20cm.

Text Solution

Verified by Experts

Given that a =24, b cm, Edge =e=20 cm
AB=(1)/(2) $\times$ Diagonal $= \frac{1}{2} \times a \sqrt{2} = (b) (\sqrt{2})$
$D C = \frac{1}{2} \times$ Diagonal $= \frac{1}{\sqrt{2} = \frac{a}{\sqrt{2}}}$
DE=DC-EC=DC-AB= $(a) (\sqrt{2}) - \frac{b}{\sqrt{2}}$
To find height h,
we have for sqare frustum
$e^{2} = h^{2} + \frac{1}{2} {(24 - 16)}^{2}$
$400 = h^{2} + \frac{1}{2} \times 8 \times = h^{2} + 32$
$h^{2} = 400 - 32 = 368 \to h = 19.18 c m$
volume $V = \frac{1}{3} h (A_{1} + \sqrt{A_{1} A_{2}} + A_{2}$
$A_{1} = a^{2} = 24^{2} = 576, A_{2} = b^{2} = 16^{2} = 256$
$V = \frac{1}{3} \times 19.18 (576 + 384 + 256) = 777.29 c m^{2}$
Total surface area =slant surface + Area of the top and bottom faces
$= \frac{1}{2}$ (sum of the perimeters $\times$ slant height + $a^{2} + b^{2}$

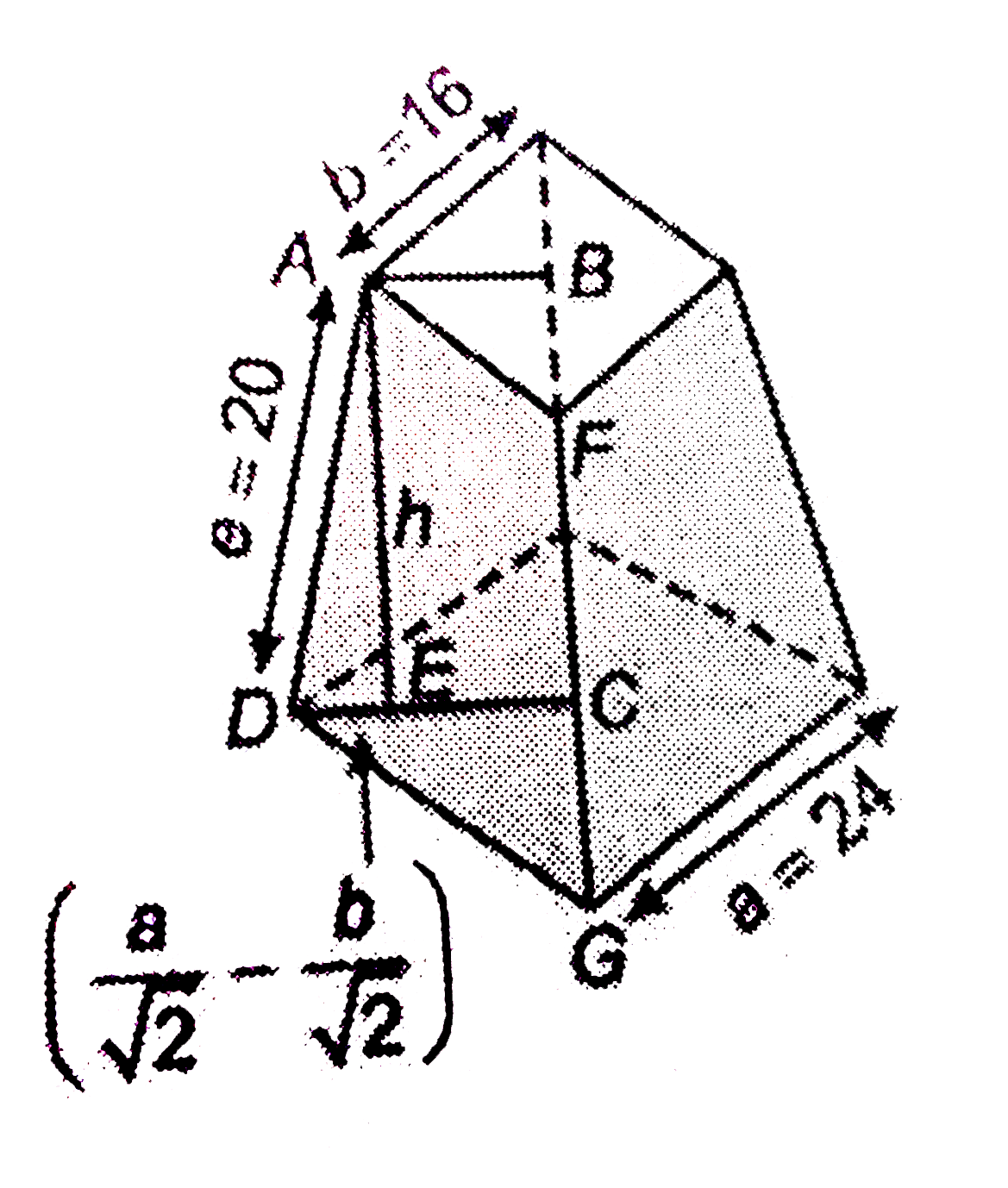
[AF=b,DG=a]
[KM=b]
But DK=MG
DK=Mg= $\frac{a - b}{2}$
$e^{2} = l^{2} + D K^{2}$
$e^{2} = l^{2} + {(\frac{a}{2} - \frac{b}{2})}^{2}$
${(20)}^{2} = l^{2} + (\frac{24}{2} \frac{16}{2^{2}}) \Rightarrow 400 = l^{2} + (4^{2})$
$[l^{2}$ =384 $\Rightarrow l = \sqrt{384}$ =19.6]
Total surface area $= \frac{1}{20} \times 4 \times 16 \times 4) \times (19.6) + 24^{2} + 16^{2}$
$= \frac{1}{2} (96 + 64) \times 19.6 + 576 + 256$
$= \frac{1}{2} \times 160 \times 19.6 + 576 + 256$
=1568+576+256=2400 $c m^{2}$

Updated on:21/07/2023

|

Class 10 MATHS SURFACE AREAS AND VOLUMES

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN-VOLUME AND SURFACE AREA OF SOLIDS-Revisions Exercise Long Answer Questions

Home
Ask Doubt
Profile