For a certain distribution, mode and median were found to be 1000 and 1250 respectively. Find mean for this distribution using an empirical relation
The correct Answer is:1375
Step by step video, text & image solution for For a certain distribution, mode and median were found to be 1000 and 1250 respectively. Find mean for this distribution using an empirical relation by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MEAN,MEDAN,MODE OF GROUPED,DATA CUMULATIVE FREQUENCY GRAPH AND OGIVE BOOK - RS AGGARWALCHAPTER - MEAN,MEDAN,MODE OF GROUPED,DATA CUMULATIVE FREQUENCY GRAPH AND OGIVE EXERCISE - Multiple Choice Questions (Mcq)
23 Videos
- MEAN,MEDAN,MODE OF GROUPED,DATA CUMULATIVE FREQUENCY GRAPH AND OGIVE BOOK - RS AGGARWALCHAPTER - MEAN,MEDAN,MODE OF GROUPED,DATA CUMULATIVE FREQUENCY GRAPH AND OGIVE EXERCISE - MUTIPLE-CHOICE QUESTIONS (MCQ)
8 Videos
- MEAN,MEDAN,MODE OF GROUPED,DATA CUMULATIVE FREQUENCY GRAPH AND OGIVE BOOK - RS AGGARWALCHAPTER - MEAN,MEDAN,MODE OF GROUPED,DATA CUMULATIVE FREQUENCY GRAPH AND OGIVE EXERCISE - EXERCISE 18 F
13 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - QUESTION
2 Videos
- PERIMETER AND AREA OF PLANE FIGURES BOOK - RS AGGARWALCHAPTER - PERIMETER AND AREA OF PLANE FIGURES EXERCISE - TEST YOURSELF (SHORT -ANSWER QUESTIONS)
1 Videos
Similar Questions
Knowledge Check
If in a frequency distribution, the mean and median are 21 and 22 respectively, then its mode is approximately
A25.5B24.0C22.0D20.5
If mode and mean of data are found 28 and 24 respectively, find median using empirical formula.
View SolutionFind the median of the following distribution
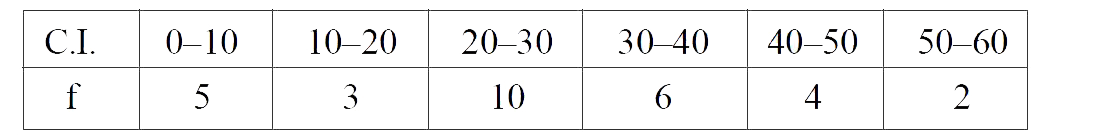
View SolutionFind the median of the following distribution
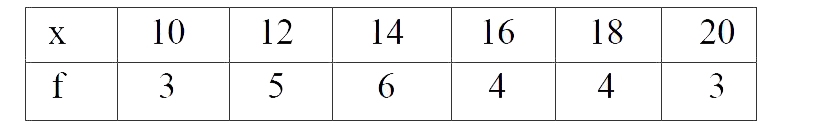
View SolutionThe mode and mean are 26.6 and 28.1 respectively in an asymmetrical distribution . Find out the value of median .
View SolutionIn an asymmetrical distribution, if the mean and median of the distribution are 270 and 220 respectively, then the mode of the data is
View SolutionThe relation between mean, mode and median is
View SolutionFind the mode of following distribution. :

View Solution