For a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
For P(x, y), we have
2≤d1(P)+d2(P)≤4
⇒2≤|x−y|√2+|x+y|√2≤4
2√2≤|x−y|+|x+y|≤4√2
In first quadrant, if x>y, we have
2√2≤x−y+x+y≤4√2
or √2≤x≤2√2
The region of points satisfying these inequalities is
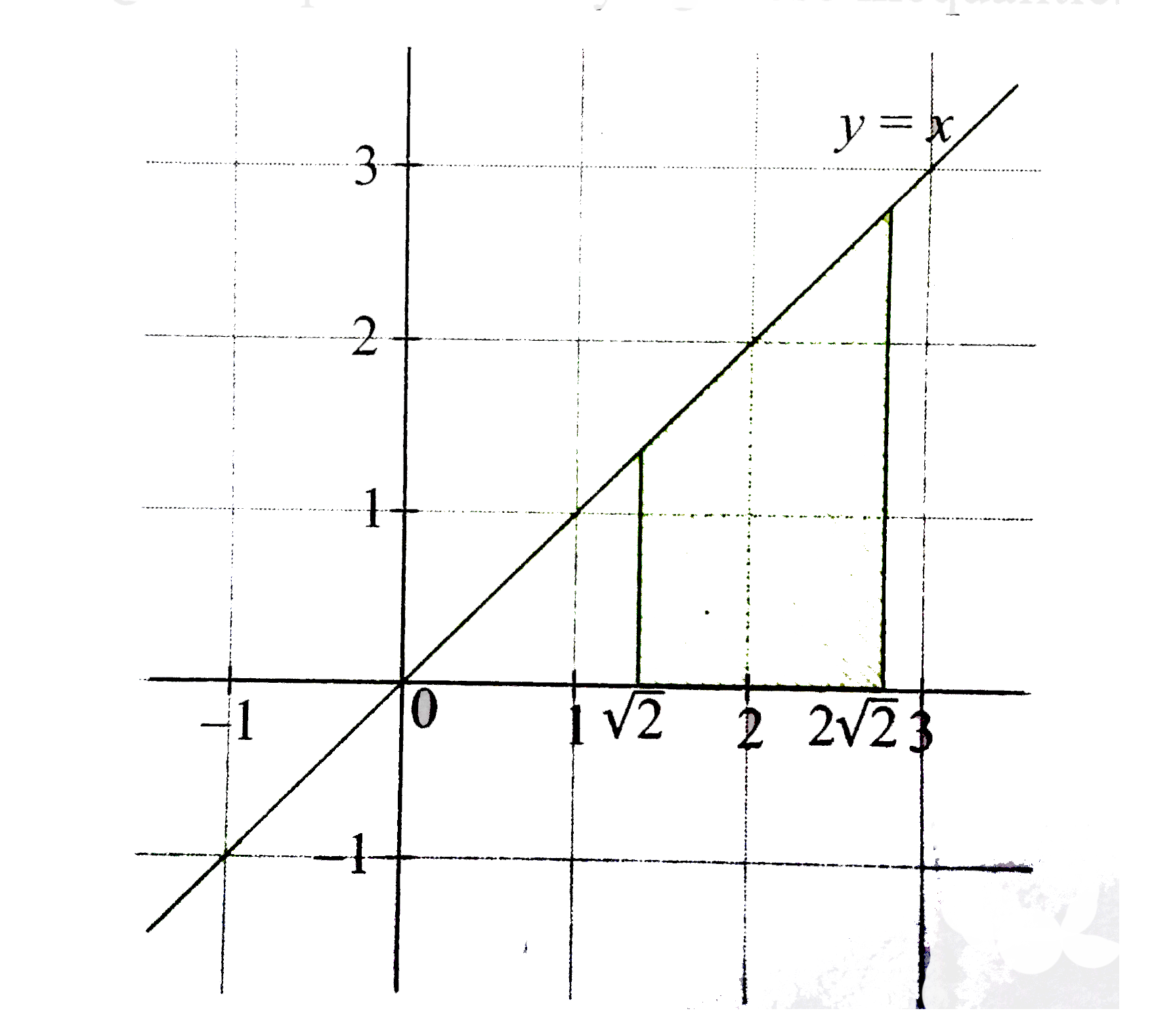
In first quadrant, if x<y, we have
or √2≤y≤2√2
The region of points satisfying these inequalities is
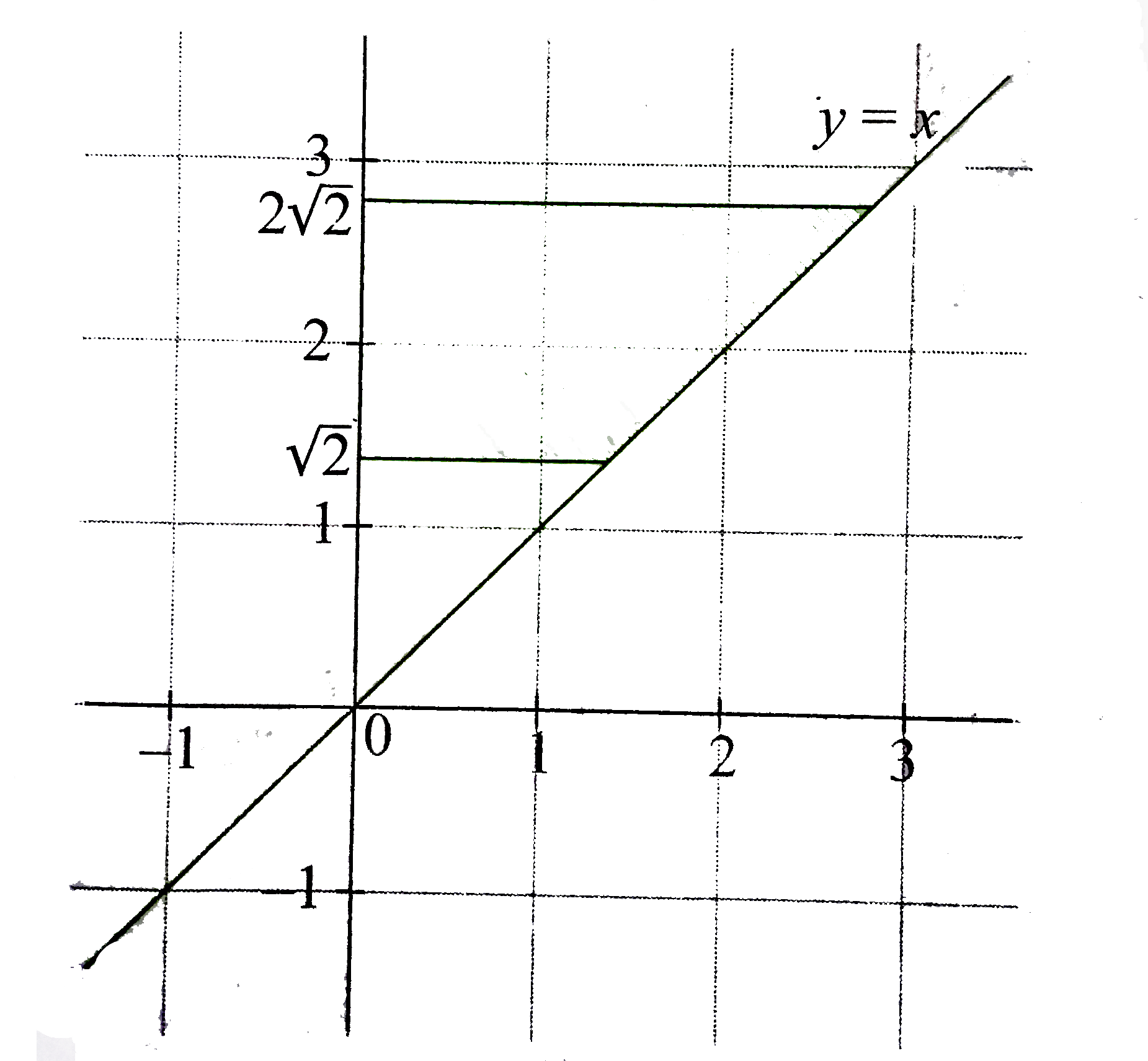
Combining above two regions, we have
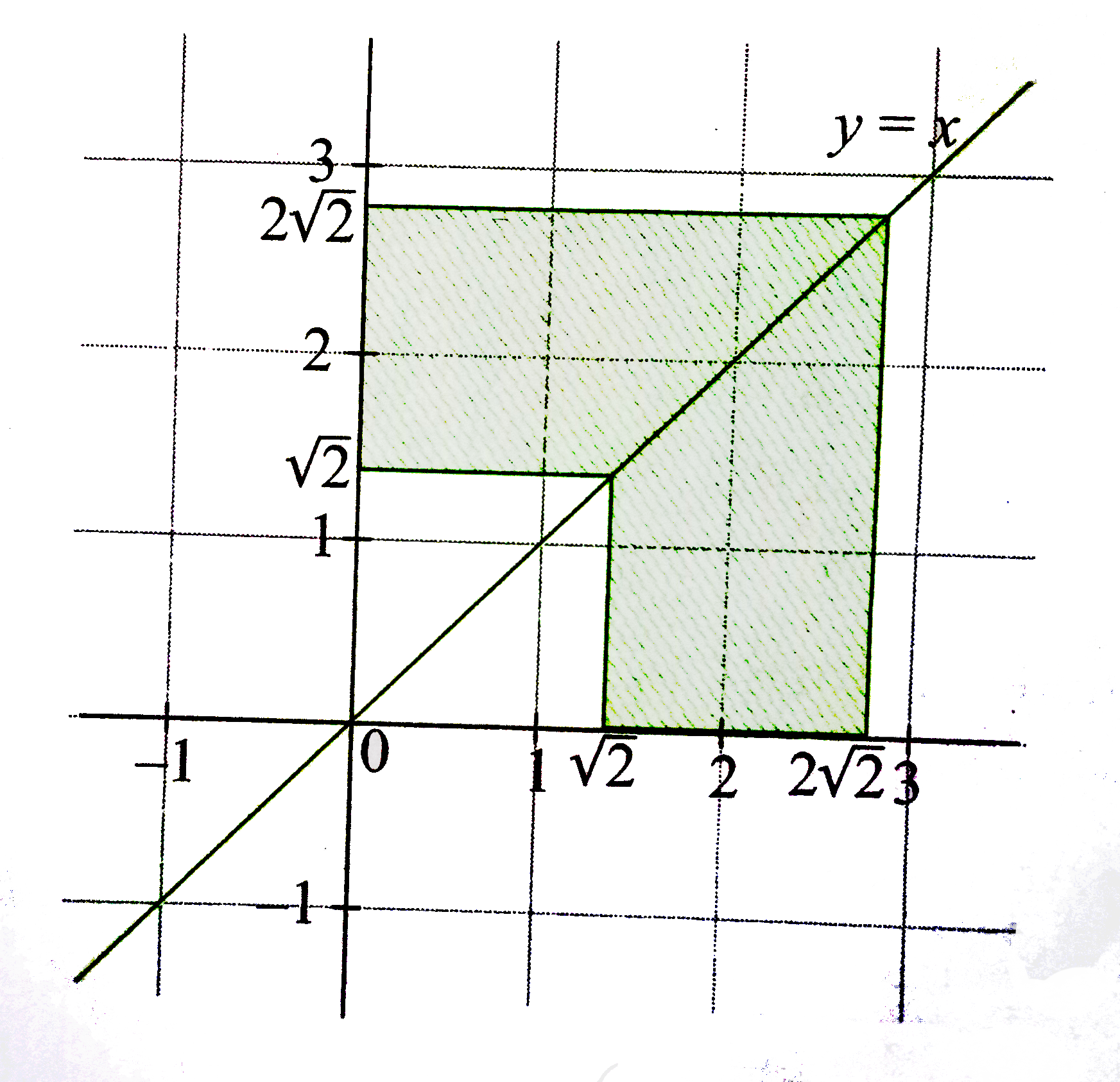
Area of shaded region =((2√2)2−(√2)2)
=8-2= 6 sq. units
Topper's Solved these Questions
Similar Questions
For a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View SolutionFor a point P in the plane, let d1 (P) and d2 (P) be the distance of the point P from the lines x – y = 0 and x + y = 0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2 < d1(P) + d2 (P)< 4, is
View Solution
Knowledge Check
- Question 1 - Select One
Let P be the set of points (x,y) such that x2≤y≤–2x+3. Then area of region bounded by points in set P is
A163B323C293D203
For a point P in the XY plane.Let d1(p),d2(p) and d3(p) be the distances of the point P from the x axis,y axis and x−y=0 respectively. If A is area of the region R consisting of all points P lying in the XY plane and satisfying d1(P)+d2(P)+√2d3(P)=5 then Which of the following is/are CORRECT
View SolutionFor a point P in the plane let d1(P)andd2 be the distance of the point P from the lines x−y=0 R consisting of all points P lying in the first quadrant of the plane and satisfying 2≥d1(P)+d2(P)≥4, is
View SolutionFor a point P(x,y),x≤2 in x−y plane moves on path y=|ax−1|+|ax−2|+ax∀α∈[0,1] If area Of region R consisting of all points P lying in the first quadrant of the plane is A when ? take it's all values α∈[0,1], then value of 6A is
View SolutionConsider a rectangle ABCD formed by the points A=(0,0), B= (6, 0), C =(6, 4) and D =(0,4), P (x, y) is a moving interior point of the rectangle, moving in such a way that d(P,AB)≤min{d(P,BC),d(P,CD)andd(P,AD)} here d (P, AB), d (P, BC), d (P, CD) and d (P, AD) represent the distance of the point P from the sides AB, BC, CD and AD respectively. Area of the region representing all possible positions of the point P is equal to
View SolutionLet the acute angle bisector of the two planes x−2y−2z+1=0and2x−3y−6+1=0 be the plane P. Then which of the following points lies on P ?
View SolutionA point P(x,y) moves so that the sum of the distance from P to the coordinate axes is equal to the distance from P to the point A(1,1). The equation of the locus of P in the first quadrant is-
View SolutionLet the acute angle bisector of the two planes x−2y−2z+1=0and2x−3y−6z+1=0 be the plane P. Then which of the following points lies on P ?
View Solution

