For acute angle $θ$ , Prove that $sin θ < θ < tan θ$ .

Text Solution

Verified by Experts

Consider the circle with unit radius as show in the following figure.
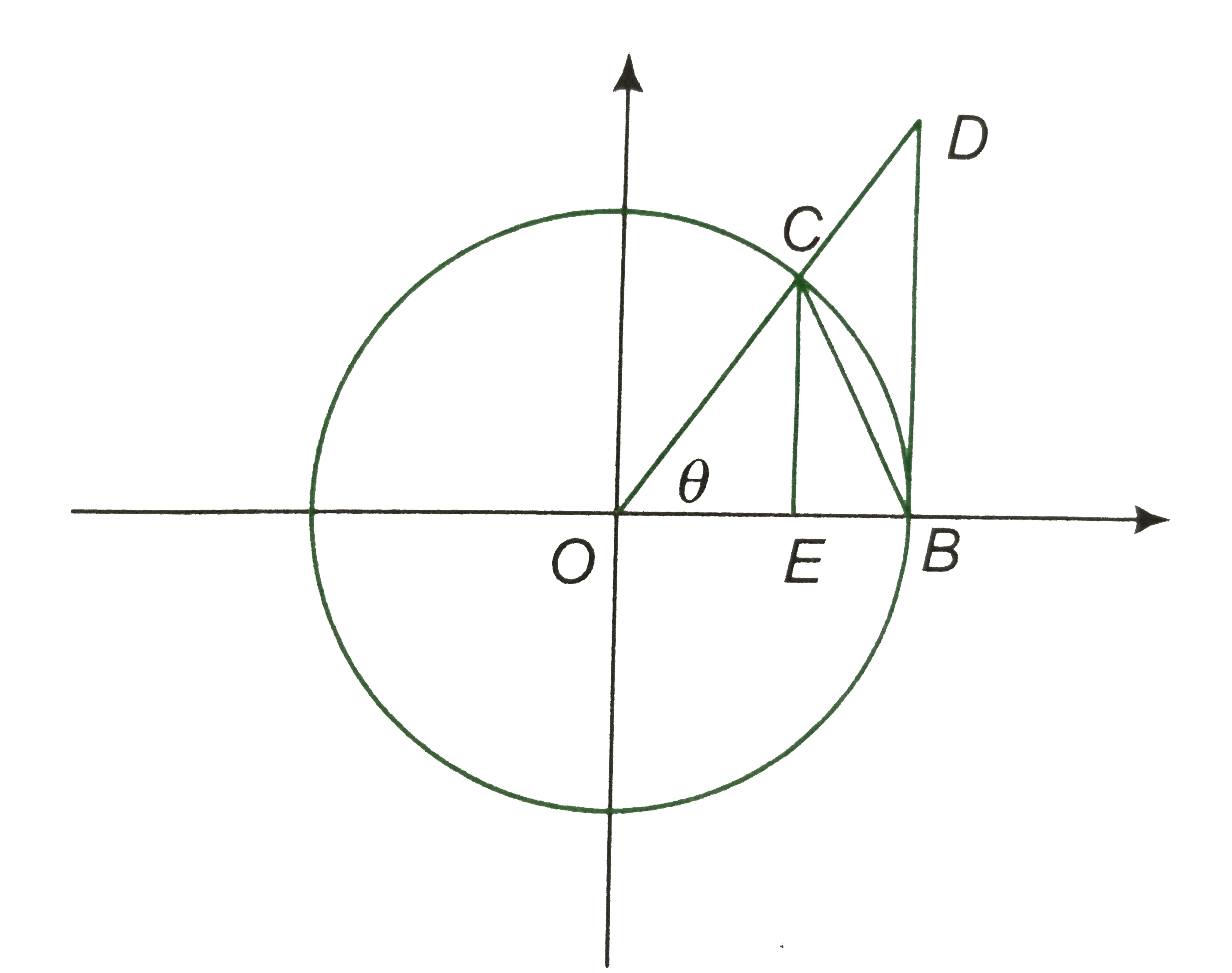From the figure, from position of C on the circle
Area of $Δ O B C < Area of sector Δ O B D$
$∴ \frac{1}{2} (C E) (O B) < \frac{1}{2} θ < \frac{1}{2} (O B) (B D)$
$\Rightarrow \frac{1}{2} (sin θ) (1) < \frac{1}{2} θ < \frac{1}{2} (1) (tan θ)$
$\Rightarrow sin θ < θ < tan θ$

|

Updated on:21/07/2023

Class 12 MATHS TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $θ$ is a positive acute angle and $tan θ + cot θ = 2$ , then the value of sec $θ$ is
A $\frac{1}{\sqrt{2}}$
B $\sqrt{2}$
C $1$
D $0$
Question 2 - Select One
If $2 θ$ is an acute angle, then the acute angle between the two lines $x^{2} (cos θ - sin θ) + 2 x y . cos θ + y^{2} (cos θ + sin θ) = 0$ is
A $2 θ$
B $\frac{θ}{2}$
C $\frac{θ}{3}$
D $(θ)$
Question 3 - Select One
If $θ$ is an acute angle and $tan θ + cot θ = 2$ , then the value of ${tan}^{5} θ + {cot}^{10} θ$ is:
A1
B2
C3
D4

CENGAGE-TRIGONOMETRIC FUNCTIONS -SINGLE CORRECT ANSWER TYPE

Home
Ask Doubt
Profile