For a≤0 , determine all real roots of the equation (1986, 5M) x2−2a|x−a|−3a2=0
Video Solution
Text Solution
We have x2−2a|x−a|−3a2=0
∵x2−3a22a=|x−a|
Roots of the equation are values of x where the graphs of ∵x2−3a22aandy=|x−|a intersect.
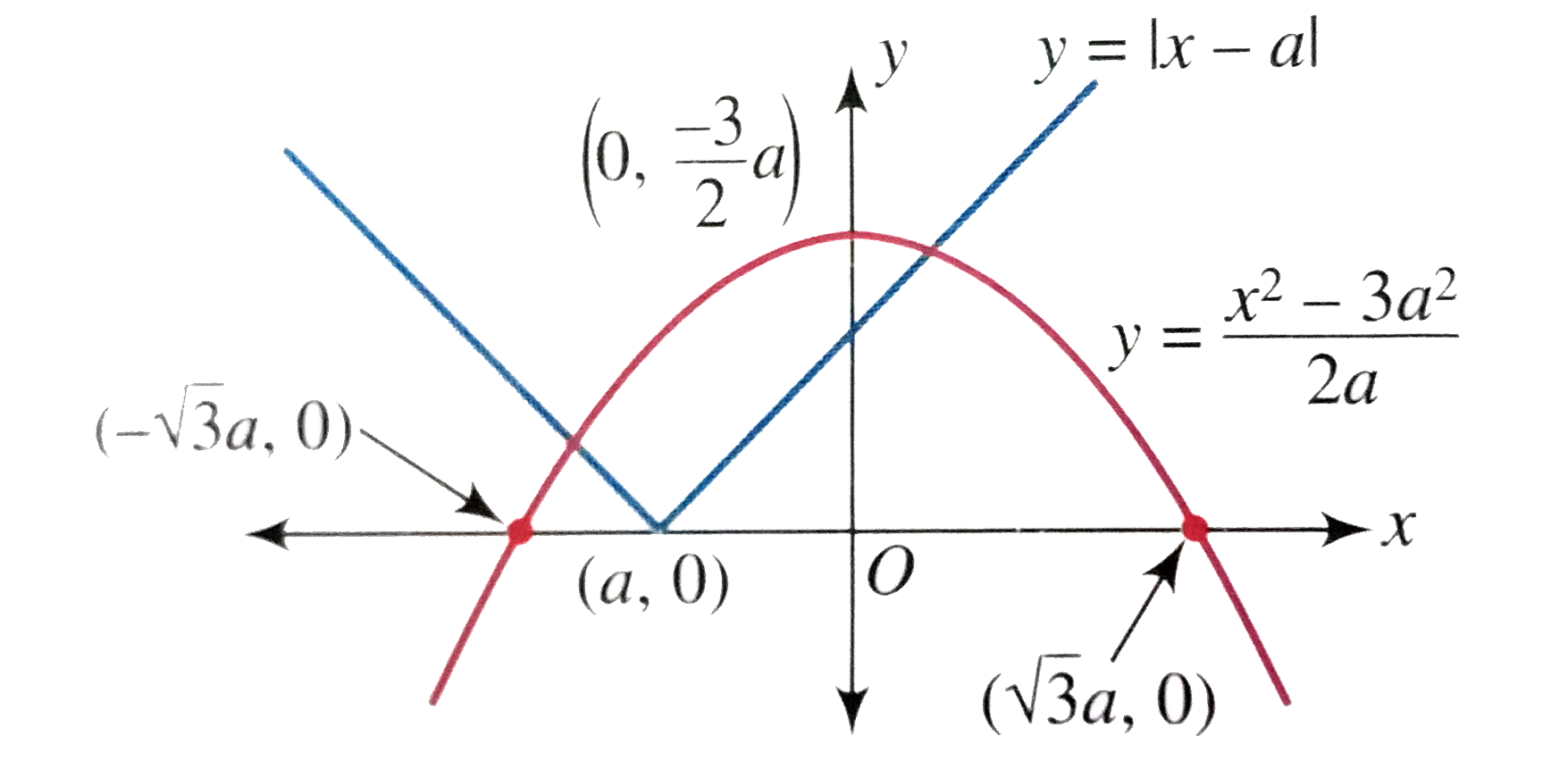
From the graph, we have x2−3a22a=a−x for x<a
and x2−3a22a=x−a for x>a
Form (i), x2−3a2=2a2−2ax
⇒x2+2ax−5a=0
⇒x=−2a±√4a2+20a22
=−2a±2a√62
=−a+a√6(asx<a)
From (ii),
x2−2a(x−a)3a2=0
⇒x2−2ax−a2=0
⇒x=2a±√4a2+4a22=a−a√2(asx>a)
Thus, the solution set is (−a+a√6,a−a√2).
|
Topper's Solved these Questions
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise
22 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
18 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise
13 Videos
Similar Questions
Knowledge Check
Find all the roots of the equation x2−5x+6=0
A2,4B2,3C1,2D2,5The sum of all real roots of the equation |x−2|2+|x−2|−2=0 is
A7B4C1D5
For a<0, deterine all real roots of the equation x2−2a|x−a|−3a2=0.
View SolutionFor a>0 ,all the real roots of the equation x2−3a|x−a|−7a2=0,are
View SolutionFor a<0, determine all solutions of the equation x2−2alx−al−3a2=0.
View SolutionThe sum of all real roots of the equation |x−3|2+|x−3|−2=0
View SolutionThe real roots of the equation |x|3−3x2+3|x|−2=0
View SolutionThe real roots of the equation |x|3−3x2+3|x|−2=0 are
View Solution
