For an ellipse x29+y24=1 with vertices A and A', drawn at the point P in the first quadrant meets the y axis in Q and the chord A'P meets the y axis in M. If 'O' is the origin then OQ2−MQ2
9
13
4
5
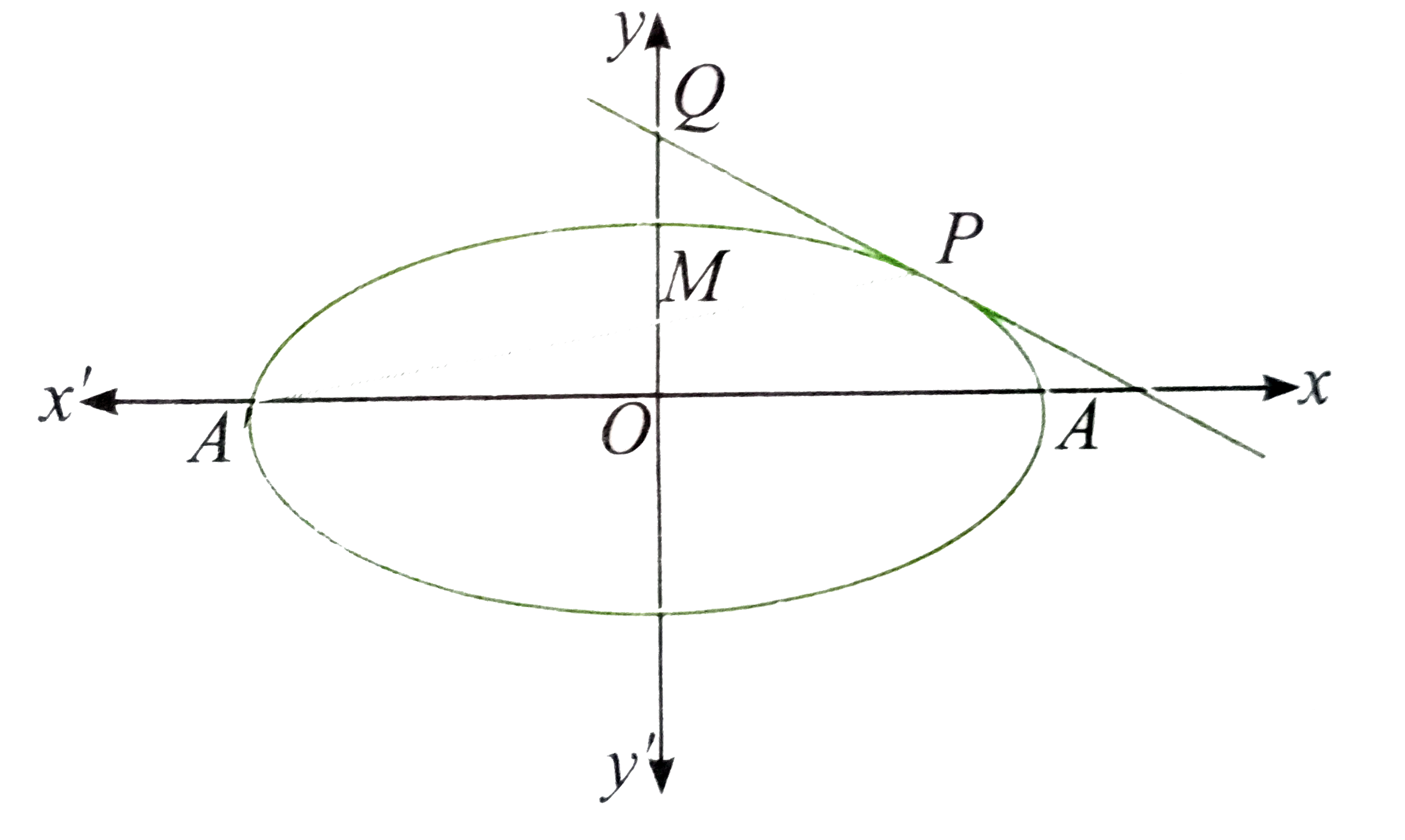
Let the P be (acosθb,sinθ)
The equation of the tangent at point P is xacosθ+ybsinθ=1
The point Q is (0,bscosecθ)
The quation of chord A'P is
y−0=bsinθacosθ+a(x+a)
Putting x=0, we have
y=bsinθcosthea+1
Then,
OQ2−MQ2=b2coses2θ−(bcosecθ−bsinθcosθ+1)2
=2b2cosθ+1−b2sinθ(cosθ+1)2
=b2cosθ+1b2sinθ(cosθ+1)2
=b2cosθ+1(2cosθ+2−sin2θcosθ+1)
=b2cosθ+1(2cosθ+1+cos2θcosθ+1)=b2=4
Similar Questions
A tangent to the ellipse x2a2+y2b2=1 touches at the point P on it in the first quadrant & meets the coordinate axes in A & B respectively. If P divides AB in the ratio 3:1 reckoning from the x-axis find the equation of the tangent.
View SolutionA tangent to the ellipse x2a2+y2b2 =1 touches at the point P on it in the first quadrant & meets the coordinate axes in A & B respectively. If P divides AB in the ratio 3 : 1 reckoning from the x-axis find the equation of the tangent.
View Solution
Knowledge Check
The straight lines ax+5y=7 and 4x+by=5 intersected in the point (2,-1), the first meets the x-axis in P and Q the second meets the y-axis in Q, then thelenght of PQ is
A10√7/6B13/6C√149/6D√99/6The tangent drawn to the hyperbola x216−y29=1, at point P in the first quadrant whose abscissa is 5, meets the lines 3x−4y=0and3x+4y=0 at Q and R respectively. If O is the origin, then the area of triangle OQR is (in square units)
A6B12C3D24The tangent to the ellipse x225+y216=1 at point P lying in the first quadrant meets x - axis at Q and y - axis at R. If the length QR is minimum, then the equation of this tangent is
A2x+√5y=6√5B√4x+2y=6√5C2x−√5=6√5D2√5x+y=6√5
Let A be the area of the region in the first quadrant bounded by the x-axis the line 2y = x and the ellipse x29+y21=1. Let A' be the area of the region in the first quadrant bounded by the y-axis the line y = kx and the ellipse . The value of 9k such that A and A' are equal is _____
View SolutionA normal drawn at a point P on the parabola y2=4ax meets the curve again at Q. The least distance of Q from the axis of the parabola, is
View SolutionLet P be a point in the first quadrant lying on the ellipse x28+y218=1. Let AB be the tangent at P to the ellipse meeting the x -axis at A and y axis at B. If O is the origin, then the minimum, possible area of ΔOAB is (in square units)
View SolutionLet F1(x1,0) and F2(x2,0), for x1<0 and x2>0, be the foci of the ellipse x29+y28=1 Suppose a parabola having vertex at the origin and focus at F2 intersects the ellipse at point M in the first quadrant and at point N in the fourth quadrant. If the tangents to the ellipse at M and N meet at R and the normal to the parabola at M meets the x-axis at Q, then the ratio of area of the triangle MQR to area of the quadrilateral MF1NF2 is
View SolutionNormal at point P(x1,y1), not lying on x-axis, to the hyperbola x2−y2=a2 meets x-axis at A and y-axis at B. If O is origin then:
View Solution
