For any 2×2 matrix, if A (adj A)=[100010] , then |A| is equal to (a) 20 (b) 100 (c) 10 (d) 0
To solve the problem, we need to find the determinant of the matrix A given that A⋅adj(A)=[100010].
1. Understand the relationship between A and its adjoint:
For any square matrix A, the product of A and its adjoint (denoted as adj(A)) is given by:
A⋅adj(A)=|A|⋅I
where |A| is the determinant of A and I is the identity matrix.
2. Set up the equation:
From the problem, we know:
A⋅adj(A)=[100010]
This can be rewritten using the relationship established:
|A|⋅I=[100010]
3. Identify the identity matrix:
The identity matrix I for a 2×2 matrix is:
I=[1001]
4. Compare both sides:
Since |A|⋅I is equal to [|A|00|A|], we can equate this to the given matrix:
[|A|00|A|]=[100010]
5. Solve for |A|:
From the above equation, we can see that:
|A|=10
6. Final answer:
Therefore, the determinant of matrix A is:
|A|=10
Conclusion:
The correct option is (c) 10.
For any square matrix A, the product of A and its adjoint (denoted as adj(A)) is given by:
A⋅adj(A)=|A|⋅I
where |A| is the determinant of A and I is the identity matrix.
From the problem, we know:
A⋅adj(A)=[100010]
This can be rewritten using the relationship established:
|A|⋅I=[100010]
The identity matrix I for a 2×2 matrix is:
I=[1001]
Since |A|⋅I is equal to [|A|00|A|], we can equate this to the given matrix:
[|A|00|A|]=[100010]
From the above equation, we can see that:
|A|=10
Therefore, the determinant of matrix A is:
|A|=10
The correct option is (c) 10.
Topper's Solved these Questions
Similar Questions
310 is equal to
View Solution1cm is equal to: (a) 0.1m (b) 0.01m (c) 0.10m (d) 0.001m
View SolutionIf [x1][10−20]=0 then x is equal to
View SolutionFor a invertible matrix A if A(adjA)=[100010] then |A|=
View SolutionIf A=[10121] , then A100 is equal to
View SolutionIn the figure, if AB=AC,∠BAD=300 and AE=AD, then x is equal to
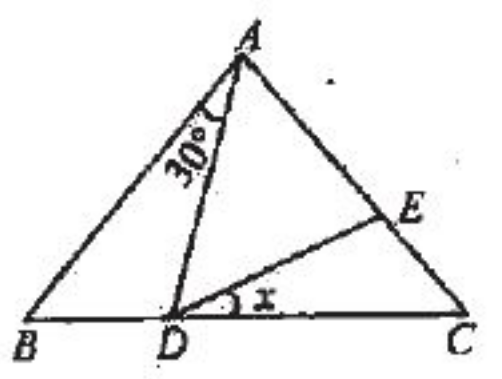
a)150 (b) 100 (c) 12.50 (d) 7.50
View SolutionIf A=⎡⎢⎣100010ab−1⎤⎥⎦ , then A2 is equal to (a) a null matrix (b) a unit matrix (c) A (d) A
View Solution2+310+5100 is equal to
(a)2.305
(b) 2.3
(c) 2.35
(d) 0.235
View SolutionIf A=⎡⎢⎣200020002⎤⎥⎦ , then A5= (a) 5A (b) 10A (c) 16A (d) 32A
View SolutionIf A=[0110], then A2 is equal to:
(a) [0110]
(b) [1001]
(c) [1010]
(d) [0011]
View Solution
