For any 2×2 matrix, if A (adj A)=[100010] , then |A| is equal to (a) 20 (b) 100 (c) 10 (d) 0
A
20
B
100
C
10
D
0
Video Solution
Text Solution
The correct Answer is:C
We know that for any square matrix A.
A(adjA)=|A|I
∴A(adjA)=[100010]=10I2⇒|A|I2=10I2⇒|A|=10
|
Topper's Solved these Questions
- MATRICESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATRICESEXERCISE - Section I - Assertion Reason Type
12 Videos
- MATRICESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATRICESEXERCISE - Exercise
79 Videos
- MATRICESBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MATRICESEXERCISE - Chapter Test
30 Videos
- LOGARITHMSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - LOGARITHMSEXERCISE - Chapter Test
21 Videos
- MEAN VALUE THEOREMSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - MEAN VALUE THEOREMSEXERCISE - Exercise
28 Videos
Similar Questions
310 is equal to
View Solution1cm is equal to: (a) 0.1m (b) 0.01m (c) 0.10m (d) 0.001m
View SolutionIf [x1][10−20]=0 then x is equal to
View SolutionFor a invertible matrix A if A(adjA)=[100010] then |A|=
View SolutionIf A=[10121] , then A100 is equal to
View SolutionIn the figure, if AB=AC,∠BAD=300 and AE=AD, then x is equal to
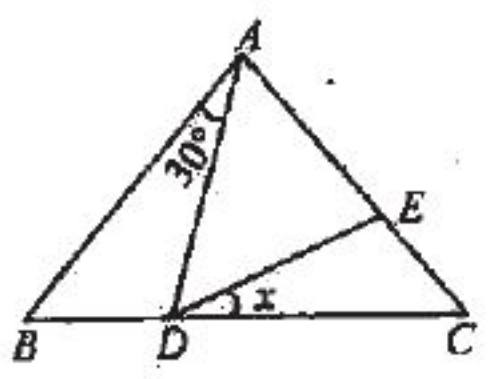
a)150 (b) 100 (c) 12.50 (d) 7.50
View SolutionIf A=⎡⎢⎣100010ab−1⎤⎥⎦ , then A2 is equal to (a) a null matrix (b) a unit matrix (c) A (d) A
View Solution2+310+5100 is equal to
(a)2.305
(b) 2.3
(c) 2.35
(d) 0.235
View SolutionIf A=⎡⎢⎣200020002⎤⎥⎦ , then A5= (a) 5A (b) 10A (c) 16A (d) 32A
View SolutionIf A=[0110], then A2 is equal to:
(a) [0110]
(b) [1001]
(c) [1010]
(d) [0011]
View Solution
