For the data
x:47834y:58635
The Karl Pearson coefficient is
63√94×66
63
63√94
none of these
The correct Answer is:A
To find the Karl Pearson coefficient of correlation (denoted as r) for the given data, we will follow these steps:
Step 1: Organize the Data
We have the following data points:
- x:4,7,8,3,4
- y:5,8,6,3,5
Let's create a table to organize this data along with the calculations we need for x2, y2, and xy.
| x | y | x2 | y2 | xy |
|---------|---------|-----------|-----------|----------|
| 4 | 5 | 16 | 25 | 20 |
| 7 | 8 | 49 | 64 | 56 |
| 8 | 6 | 64 | 36 | 48 |
| 3 | 3 | 9 | 9 | 9 |
| 4 | 5 | 16 | 25 | 20 |
| Total | | 154 | 159 | 153 |
Step 2: Calculate Required Sums
- n=5 (the number of data points)
- Σx=4+7+8+3+4=26
- Σy=5+8+6+3+5=27
- Σx2=16+49+64+9+16=154
- Σy2=25+64+36+9+25=159
- Σxy=20+56+48+9+20=153
Step 3: Use the Formula for Karl Pearson Coefficient
The formula for the Karl Pearson coefficient r is given by:
r=nΣxy−ΣxΣy√(nΣx2−(Σx)2)(nΣy2−(Σy)2)
Step 4: Substitute the Values
Now we will substitute the calculated values into the formula:
r=5⋅153−26⋅27√(5⋅154−262)(5⋅159−272)
Calculating each part:
1. nΣxy=5⋅153=765
2. ΣxΣy=26⋅27=702
3. nΣx2=5⋅154=770
4. (Σx)2=262=676
5. nΣy2=5⋅159=795
6. (Σy)2=272=729
Now substituting these values:
r=765−702√(770−676)(795−729)
Calculating the differences:
1. 765−702=63
2. 770−676=94
3. 795−729=66
Now substituting back:
r=63√94⋅66
Calculating 94⋅66=6204:
r=63√6204≈6378.8≈0.799
Final Result
Thus, the Karl Pearson coefficient r is approximately 0.799.
We have the following data points:
- x:4,7,8,3,4
- y:5,8,6,3,5
|---------|---------|-----------|-----------|----------|
| 4 | 5 | 16 | 25 | 20 |
| 7 | 8 | 49 | 64 | 56 |
| 8 | 6 | 64 | 36 | 48 |
| 3 | 3 | 9 | 9 | 9 |
| 4 | 5 | 16 | 25 | 20 |
| Total | | 154 | 159 | 153 |
- n=5 (the number of data points)
- Σx=4+7+8+3+4=26
- Σy=5+8+6+3+5=27
- Σx2=16+49+64+9+16=154
- Σy2=25+64+36+9+25=159
- Σxy=20+56+48+9+20=153
The formula for the Karl Pearson coefficient r is given by:
Now we will substitute the calculated values into the formula:
2. ΣxΣy=26⋅27=702
3. nΣx2=5⋅154=770
4. (Σx)2=262=676
5. nΣy2=5⋅159=795
6. (Σy)2=272=729
2. 770−676=94
3. 795−729=66
Thus, the Karl Pearson coefficient r is approximately 0.799.
Topper's Solved these Questions
- CORRELATION AND REGRESSION BOOK - ML KHANNACHAPTER - CORRELATION AND REGRESSION EXERCISE - PROBLEM SET (1) (TRUE AND FALSE)
9 Videos
- CONCEPTS OF SET THEORY BOOK - ML KHANNACHAPTER - CONCEPTS OF SET THEORY EXERCISE - Self Assessment Test
13 Videos
- DEFINITE INTEGRALBOOK - ML KHANNACHAPTER - DEFINITE INTEGRALEXERCISE - Miscellaneous Questions (Assertion/Reason)
1 Videos
Similar Questions
From the following data, determine Karl Pearson's coefficient of correlation between X and Y series for 15 pairs .
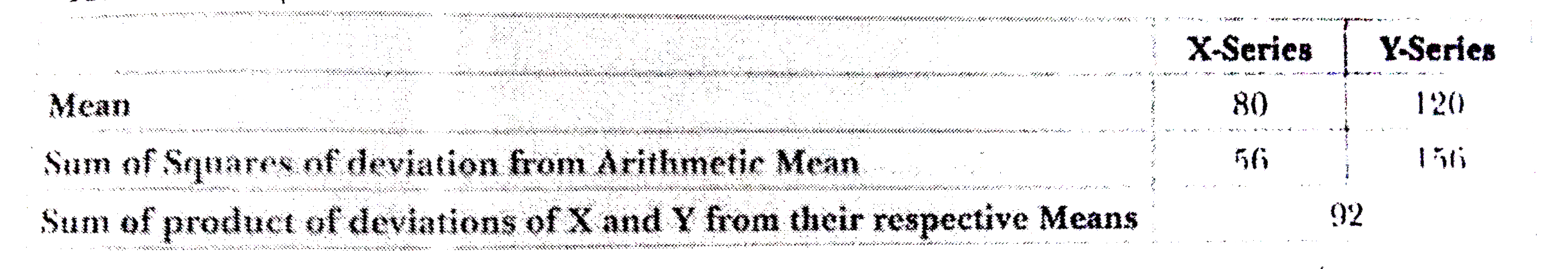
View SolutionFrom the following data, compute Karl Pearson coefficient of correlation :
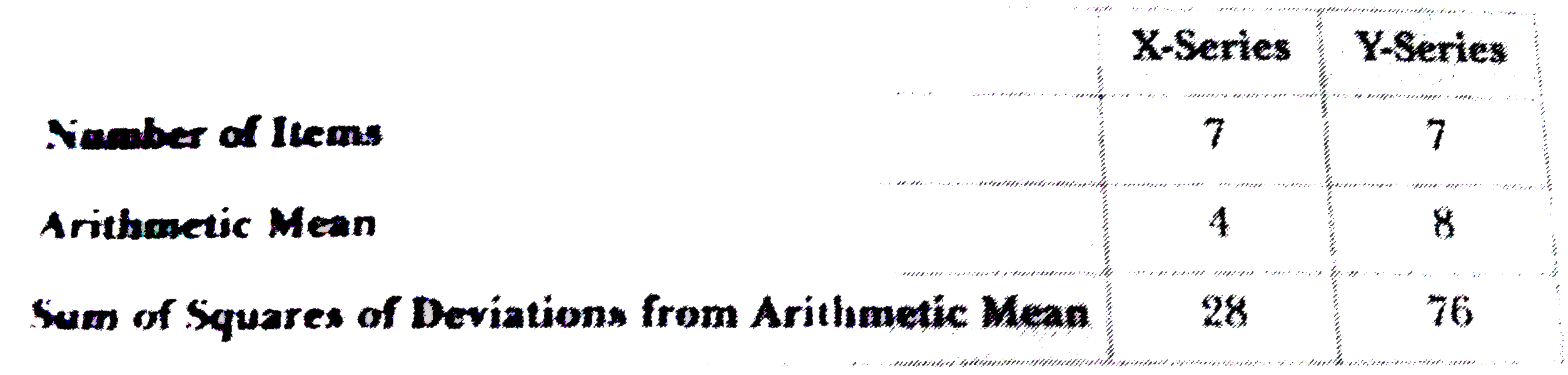
Summation of product of deviation of X and Y series from their respective means is 46
View Solution
Knowledge Check
Consider the following data :
x57846y24324
What is the regression equation of y on x?Ay=0.6+0.4xBy=0.7+0.3xCy=6+5xDy=4+9xIf x:348621y:539692
The coefficient of correrlation will be approximatelyA0.49B−0.49C0.40D−0.40What is quartile deviation for the datsa x23456f34841
A0B14C12D1
Median of the data
4,5,9,2,6,8,7 is 2
View SolutionConsider the data 2,3,2,4,5,6 , 4, 2, 3, 3, 7 , 8 , 2,2 . The frequency of 2 is _______
View SolutionThe median of the data : 3, 4, 5, 6, 7, 3, 4 is
View SolutionFind the mode from the following data :
5,8,4,5,5,8,4,7,8,5
View SolutionIf A=⎡⎢⎣345678⎤⎥⎦andB=[357468]. Then which one of following is correct ?
View Solution
