Question

For the following assignment problem minimize total man hours:

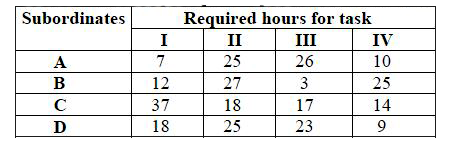
Subtract the ____element of each ____From very element of that_____

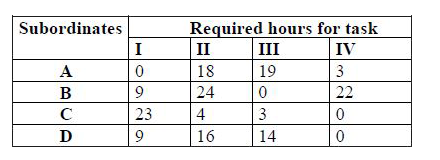
Subtract the smallest element in each column from_______
of that column.

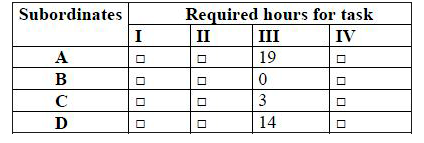
The lines covering all zeros is ______to the order of matrix______.The assignment is made as follows:

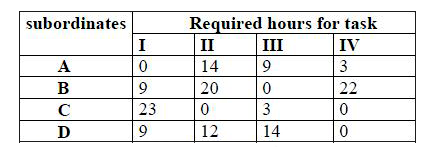
Optimum solution is shown as follows:
$A\to \square ,\square \to III,C\to \square ,\square \to IV$
Minimum hours required is ______hours.

Answer

37 hours