For the following distribution, calculate the mean using all suitable methods: Size of item: 1-4 4-9 9-16 16-27 Frequency: 6 12 26 20
To calculate the mean of the given distribution using different methods, we will follow these steps:
Given Data:
- Size of item (Class Intervals): 1-4, 4-9, 9-16, 16-27
- Frequency (f): 6, 12, 26, 20
Step 1: Calculate Midpoints (Xi) of Each Class Interval
The midpoint for each class interval can be calculated using the formula:
Xi=Lower limit+Upper limit2
- For the interval 1-4:
Xi=1+42=2.5
- For the interval 4-9:
Xi=4+92=6.5
- For the interval 9-16:
Xi=9+162=12.5
- For the interval 16-27:
Xi=16+272=21.5
Step 2: Create a Table for Frequencies and Midpoints
| Class Interval | Frequency (f) | Midpoint (Xi) | f * Xi |
|----------------|---------------|----------------|--------|
| 1 - 4 | 6 | 2.5 | 15 |
| 4 - 9 | 12 | 6.5 | 78 |
| 9 - 16 | 26 | 12.5 | 325 |
| 16 - 27 | 20 | 21.5 | 430 |
Step 3: Calculate f * Xi for Each Class
- For the first interval: 6×2.5=15
- For the second interval: 12×6.5=78
- For the third interval: 26×12.5=325
- For the fourth interval: 20×21.5=430
Step 4: Calculate the Summation of Frequencies and f * Xi
- Summation of frequencies (N):
N=6+12+26+20=64
- Summation of f * Xi:
Σ(f∗Xi)=15+78+325+430=848
Step 5: Calculate the Mean
Using the formula for mean:
Mean=Σ(f∗Xi)N
Mean=84864=13.25
Method 2: Assumed Mean Method
1. Assume a Mean (A): Let A=6.5 (the midpoint of the second class interval).
2. Calculate Deviations (ui):
- For 1-4: u1=2.5−6.5=−4
- For 4-9: u2=6.5−6.5=0
- For 9-16: u3=12.5−6.5=6
- For 16-27: u4=21.5−6.5=15
3. Create a Table for Frequencies and Deviations:
| Class Interval | Frequency (f) | Deviation (ui) | f * ui |
|----------------|---------------|----------------|--------|
| 1 - 4 | 6 | -4 | -24 |
| 4 - 9 | 12 | 0 | 0 |
| 9 - 16 | 26 | 6 | 156 |
| 16 - 27 | 20 | 15 | 300 |
4. Calculate f * ui:
- For the first interval: 6×−4=−24
- For the second interval: 12×0=0
- For the third interval: 26×6=156
- For the fourth interval: 20×15=300
5. Calculate Summation of f * ui:
Σ(f∗ui)=−24+0+156+300=432
6. Calculate Mean Using Assumed Mean Method:
Using the formula:
Mean=A+Σ(f∗ui)N
Mean=6.5+43264
Mean=6.5+6.75=13.25
Final Result
The mean calculated using both methods is:
Mean=13.25
- Size of item (Class Intervals): 1-4, 4-9, 9-16, 16-27
- Frequency (f): 6, 12, 26, 20
The midpoint for each class interval can be calculated using the formula:
Xi=Lower limit+Upper limit2
Xi=1+42=2.5
- For the interval 4-9:
Xi=4+92=6.5
- For the interval 9-16:
Xi=9+162=12.5
- For the interval 16-27:
Xi=16+272=21.5
| Class Interval | Frequency (f) | Midpoint (Xi) | f * Xi |
|----------------|---------------|----------------|--------|
| 1 - 4 | 6 | 2.5 | 15 |
| 4 - 9 | 12 | 6.5 | 78 |
| 9 - 16 | 26 | 12.5 | 325 |
| 16 - 27 | 20 | 21.5 | 430 |
- For the first interval: 6×2.5=15
- For the second interval: 12×6.5=78
- For the third interval: 26×12.5=325
- For the fourth interval: 20×21.5=430
- Summation of frequencies (N):
N=6+12+26+20=64
Σ(f∗Xi)=15+78+325+430=848
Using the formula for mean:
Mean=Σ(f∗Xi)N
Mean=84864=13.25
1. Assume a Mean (A): Let A=6.5 (the midpoint of the second class interval).
2. Calculate Deviations (ui):
- For 1-4: u1=2.5−6.5=−4
- For 4-9: u2=6.5−6.5=0
- For 9-16: u3=12.5−6.5=6
- For 16-27: u4=21.5−6.5=15
| Class Interval | Frequency (f) | Deviation (ui) | f * ui |
|----------------|---------------|----------------|--------|
| 1 - 4 | 6 | -4 | -24 |
| 4 - 9 | 12 | 0 | 0 |
| 9 - 16 | 26 | 6 | 156 |
| 16 - 27 | 20 | 15 | 300 |
- For the first interval: 6×−4=−24
- For the second interval: 12×0=0
- For the third interval: 26×6=156
- For the fourth interval: 20×15=300
Σ(f∗ui)=−24+0+156+300=432
Using the formula:
Mean=A+Σ(f∗ui)N
Mean=6.5+43264
Mean=6.5+6.75=13.25
The mean calculated using both methods is:
Mean=13.25
Topper's Solved these Questions
Similar Questions
Find the value of for the following distribution whose mean is 16.6.
View SolutionUsing step-deviation method, calculate the mean marks of the following distribution.
 View Solution
View SolutionUsing step deviation method, calculate the mean marks of the following distribution.
 View Solution
View SolutionFind the missing frequency for the following distribution whose mean is 7.68
x:3 5 7 9 11 13
y:6 8 15 p 8 4View SolutionFind the value of p for the following distribution whose mean is 16.6 8 12 15 20 25 30 12 16 20 24 16 8 4
View SolutionCalculate the mean for the following distribution: 5 6 7 8 9 4 8 14 11 3
View SolutionCalculate the mean deviation about the median of the following frequency distribution: 5 7 9 11 13 15 17 Having Frequency 2 4 6 8 10 12 8
View SolutionCalculate the mean for the following distribution: x : 5 6 7 8 9 f : 4 8 14 11 3
View SolutionUsing direct method, find the mean of following frequency distribution:
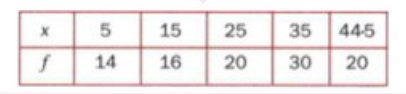 View Solution
View SolutionFind the mean of the following frequency distribution, using step-deviation method: Class 0-10 10-20 20-30 30-40 40-50 Frequency 7 12 13 10 8
View Solution

