For the following distribution

the sum of lower limits of the median class and modal class is
15
25
30
35
The correct Answer is:B
Here,

Now, N2=662=33, Which lies in the interval 10-15. Therefore, lower limit of the mediuan class is 10. The highest frequency is 20, which lies in the interval 15-20. Therefore lower limit modal class is 15. Hence, required sum is 10+15=25.
Topper's Solved these Questions
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - VERY SHORT ANSWERS QUESTIONS
14 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - SHORT ANSWERS QUESTIONS
42 Videos
- REAL NUMBERSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - REAL NUMBERSEXERCISE - LONG ANSWER TYPE QUESTIONS
5 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS
20 Videos
Similar Questions
For the following distribution

the modal class is
View SolutionConsider the following frequency distribution

The upper limit of the median class in
View SolutionFor the following frequency distribution

The upper limit of median class is
View SolutionState the modal class.

View SolutionWhile calculating mode the following observation are found. Lower limit of modal class =40, frequency of modal class =20, frequency of previous class =12 , frequency of preceding class =11 and width of the class =10, find mode .
View SolutionFind the median for the following distribution :
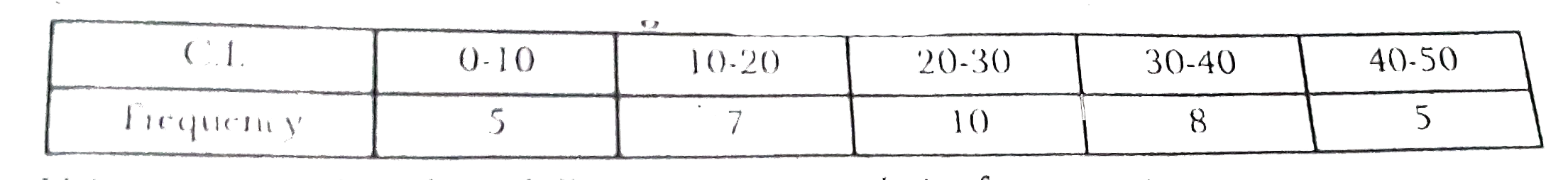
View SolutionConsider the data

The frequency of the upper limit of the median class and the lower limit of the modal class is
View SolutionIn the following data, find the values of a and b . Find the median class modal class :

View SolutionConsider the following distribution
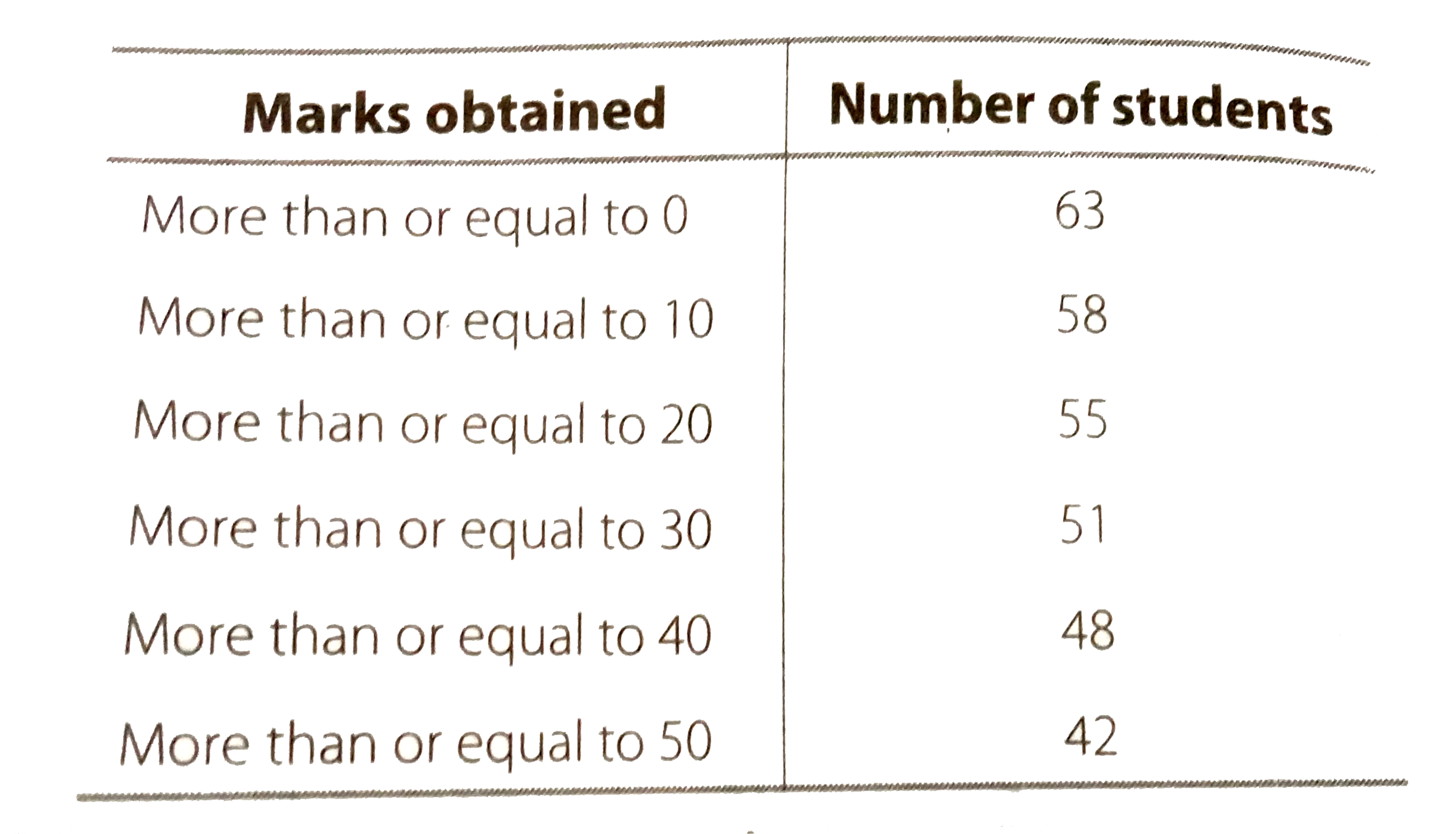
Frequency of the class 30-40 is
View SolutionThe following distributions represent the height of 160 studens of a class :

Find the modal height
View Solution
