For the function f(x)=x4(12(log)ex−7), the point (1,7) is the point of inflection. x=e13 is the point of minima the graph is concave downwards in (0,1) the graph is concave upwards in (1,∞)Solution in Bengali
the point (1,-7) is the point of minima
x=e1/3 is the point of minima
the graph is concave downwards in (0,1)
the graph is concave upwards in (1,∞)
The correct Answer is:1,2,3,4
y=f(x)=x4(12logex−7),x>0
∴dydx=16x3(3logex−1)andd2ydx216x2(9logex)
dydx=0→x=e1/3
Atx=−e1/3,d2ydx2>0,hence x=e1/3 is point of minima
Also for 0<x<1,d2ydx2<0 and for x>1,d2ydx2>0
Hence x =1 is point of inflection and for <x<1 graph is concave downward and for x>1 graph is concave upward.
Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Linked comprehension type
50 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Matrix Match Type
11 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise
92 Videos
- METHODS OF DIFFERENTIATIONBOOK - CENGAGE PUBLICATIONCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Multiple Correct Answer Type
7 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
Similar Questions
f(x)=sin−1x+x2−3x+x33,x∈[0,1]
View Solutionconsider function f(x) =x4−14x2+24x−3. Now match the following lists:

View SolutionA function is matched below against an interval where it is supposed to be increasing. Which of the following parts is incorrectly matched? Interval, Function [2, ∞) , 2x3−3x2−12x+6 (−∞,∞) , x3=3x2+3x+3 (−∞−4) , x3+6x2+6 (−∞,13) , 3x2−2x+1
View SolutionIf y=cos−1√√1+x2+12√1+x2,thendydxisequa<o 12(1+x2),x∈R (b) 12(1+x2),x>0 −12(1+x2),x<0 (d) 12(1+x2),x<0
View SolutionLet f:R→R,y=f(x),f(0)=0,f'(x)>0andf''(x)>0. Three point A(α,f(α)),B(β,f(β)),C(γ,f(γ))ony=f(x) such that 0<α<β<γ.
Which of the following is false ?
View SolutionFor the function f(x)=x4(12(log)ex−7), the point (1,7) is the point of inflection. x=e13 is the point of minima the graph is concave downwards in (0,1) the graph is concave upwards in (1,∞)
View SolutionThe graph of y = f' (x) is shown. Find the point of local maxima, local minima and the point of inflection of f(x).

View SolutionConcavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
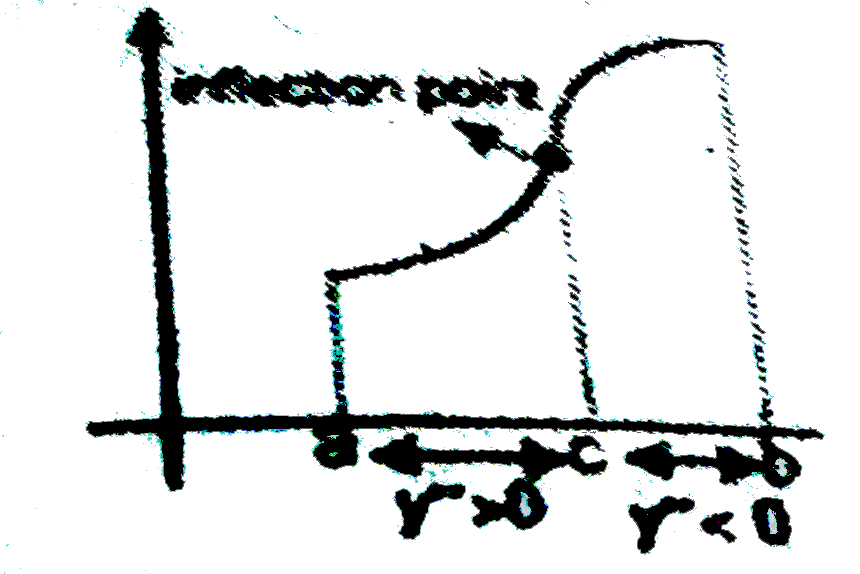
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :
View SolutionDraw the graph of f(x)=ln(1−ln x). Find the point of inflection.
View SolutionStatement I :If f(x) is increasing function with upward concavity, then concavity of f−1(x) is also upwards.
Statement II : If f(x) is decreasing function with upwards concavity, then concavity of f−1(x) is alo upwards.
View SolutionDetermine the intervals of concavity of the curve f(x)=(x−1)3(x−5),x∈R and , points of inflection if any
View SolutionFor the function f(x)=x4(12(log)ex−7), the point (1,7) is the point of inflection. x=e13 is the point of minima the graph is concave downwards in (0,1) the graph is concave upwards in (1,∞)
View SolutionDraw the graph of f(x)=ln(1−ln x). Find the point of inflection.
View SolutionFind the intervals in which the graphs of the following functions are concave or convex and locate the points of inflection :
y=x4+x3−18x2+24x−12,
View SolutionFind the intervals in which the graphs of the following functions are concave or convex and locate the points of inflection :
y=x1+x2
View SolutionFind the intervals in which the graphs of the following functions are concave or convex and locate the points of inflection :
y=x+x2/3
View Solution
