For △ABC≅△ACB, then
AB=AC
AB=BC
AC=BC
None of these
The correct Answer is:A
To solve the problem, we need to analyze the congruence of the two triangles given: triangle ABC and triangle ACB.
1. Understand Triangle Congruence:
- When two triangles are congruent, it means that their corresponding sides and angles are equal.
2. Identify the Triangles:
- We have triangle ABC and triangle ACB. The letters indicate the vertices of the triangles.
3. Corresponding Sides:
- For triangle ABC:
- Side AB corresponds to side AC.
- Side BC corresponds to side CB.
- Side AC corresponds to side AB.
- Therefore, we can establish the following equalities:
- AB = AC
- BC = CB (which is the same side)
- AC = AB
4. Corresponding Angles:
- The angles of the triangles also correspond as follows:
- Angle A (in triangle ABC) corresponds to Angle A (in triangle ACB).
- Angle B (in triangle ABC) corresponds to Angle C (in triangle ACB).
- Angle C (in triangle ABC) corresponds to Angle B (in triangle ACB).
- Thus, we have:
- Angle A = Angle A
- Angle B = Angle C
- Angle C = Angle B
5. Evaluating the Options:
- Now, we need to evaluate the options provided in the question:
- Option 1: AB = AC (This is correct as established).
- Option 2: AB = BC (This is incorrect since BC = CB, not equal to AB).
- Option 3: AC = BC (This is incorrect since BC = CB, not equal to AC).
- Option 4: None of these (This is incorrect since Option 1 is correct).
6. Conclusion:
- The correct option is Option 1: AB = AC.
- When two triangles are congruent, it means that their corresponding sides and angles are equal.
- We have triangle ABC and triangle ACB. The letters indicate the vertices of the triangles.
- For triangle ABC:
- Side AB corresponds to side AC.
- Side BC corresponds to side CB.
- Side AC corresponds to side AB.
- Therefore, we can establish the following equalities:
- AB = AC
- BC = CB (which is the same side)
- AC = AB
- The angles of the triangles also correspond as follows:
- Angle A (in triangle ABC) corresponds to Angle A (in triangle ACB).
- Angle B (in triangle ABC) corresponds to Angle C (in triangle ACB).
- Angle C (in triangle ABC) corresponds to Angle B (in triangle ACB).
- Thus, we have:
- Angle A = Angle A
- Angle B = Angle C
- Angle C = Angle B
- Now, we need to evaluate the options provided in the question:
- Option 1: AB = AC (This is correct as established).
- Option 2: AB = BC (This is incorrect since BC = CB, not equal to AB).
- Option 3: AC = BC (This is incorrect since BC = CB, not equal to AC).
- Option 4: None of these (This is incorrect since Option 1 is correct).
- The correct option is Option 1: AB = AC.
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLESEXERCISE - PART-A (Fill in the blanks )10videos
TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLESEXERCISE - PART-A (State which of the following statements are true and false )5videos
TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Practice Test8videos
SURFACE AREAS AND VOLUMES
Similar Questions
Knowledge Check
- Question 1 - Select One
If △ABC≅△DEF then
AAC=DEBBC=DFCFE=CBDAB=DF - Question 2 - Select One or More
If △CAB≅△MLK then ∠K = _______
A∠AB∠BC∠CDNone of these
If △ABC≅△DEF then
∠E = ______View SolutionIf △ABC≅△DEF then
BC = ________View SolutionIf △ABC≅△DEF then
∠EDF=________View SolutionIf △ABC≅△DEF then
∠BCA=_______View SolutionIn quadrilateral ACBD, AC=AD and AB bisects ∠A. Show that △ABC≅△ABD. What can you say about BC and BD?
View SolutionIn the given figure, figure, if ∠1=∠2 and △NSQ≅△MTR, then prove that △PTS~△PRQ.
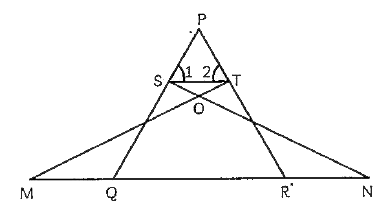 View Solution
View Solution

