For what values of x the function f(x)=x4−4x3+4x2+40 is monotonic decreasing?
A
0<x<1
B
1<x<2
C
2<x<3
D
4<x<5
Video Solution
Text Solution
The correct Answer is:B
Given f(x)=x4−4x3+4x2+40
⇒f'(x)=4x3−12x2+8x
For monotonic decreasing f'(x)<0
⇒x(4x2−12x+8)<0
⇒x(x2−3x+2)<0
⇒x(x−1)(x−2)<0
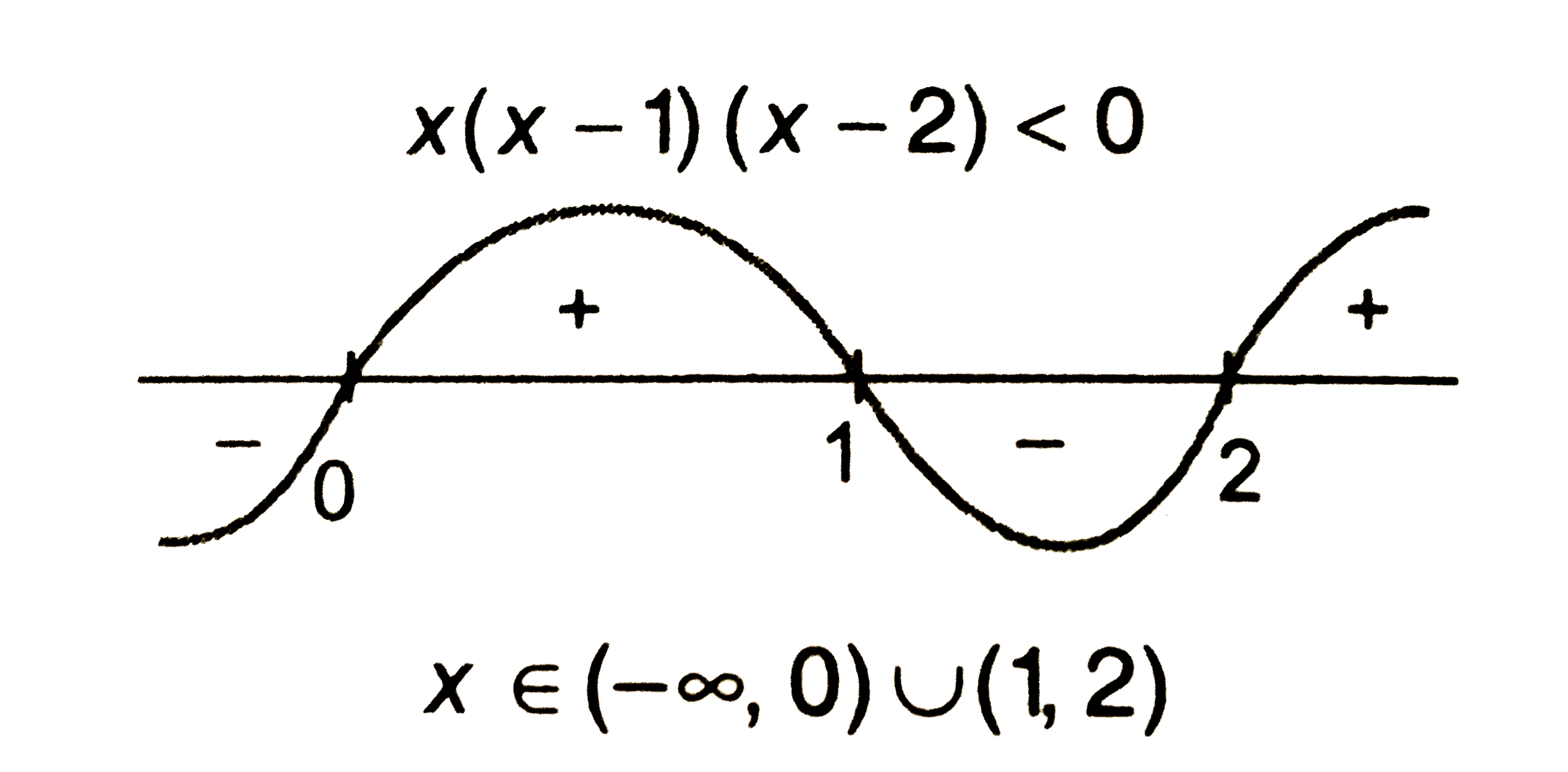
∴xε(−∞,0)∪(1,2)
|
Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVESBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - MHT CET CORNER
21 Videos
- APPLICATIONS OF DERIVATIVESBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - MHT CET CORNER
21 Videos
- APPLICATIONS OF DEFINITE INTEGRALS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner
6 Videos
- BINOMIAL DISTRIBUTIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - BINOMIAL DISTRIBUTIONEXERCISE - MHT CET Corner
6 Videos
Similar Questions
Knowledge Check
For what values of x the function f(x)=x4−4x3+4x2+40 is monotonically increasing ?
A0<x<1B1<x<2C2<x<3D4<x<5For what values of x the function f(x)=x4−4x3+40 si monotonic decreassing?
A0<x<1B1<x<2C2<x<3D4<x<5For what values of x, the function f(x)=x+4x2 is monotonically decreasing
Ax<0Bx>2Cx<2D0<x<2
