For which of the following conditions the construction of a triangle is NOT possible?
If two sides and one angle is given.
If two sides and included angle between them is given.
If three sides are given.
If two angles and side between them is given.
The correct Answer is:A
To determine the conditions under which the construction of a triangle is not possible, we will analyze each of the given options step by step.
1. Option A: Two sides and one angle (not included)
- Given two sides (let's say AB and AC) and an angle (∠A) that is not between them.
- In this case, we can draw the two sides AB and AC from point A, but we cannot determine where point C will lie because the angle is not included between the two sides.
- Therefore, we cannot complete the triangle construction as we do not know the position of point C.
- Conclusion: Triangle construction is not possible with this condition.
2. Option B: Two sides and an included angle
- Given two sides (let's say AB and AC) and the included angle (∠A).
- Here, we can construct the triangle by drawing side AB and then using the angle ∠A to determine the position of point C.
- Conclusion: Triangle construction is possible with this condition.
3. Option C: Three sides
- Given three sides (let's say lengths a, b, and c).
- We can construct the triangle by drawing one side (say AB), and then using the lengths of the other two sides to find point C.
- Conclusion: Triangle construction is possible with this condition.
4. Option D: Two angles and the side between them
- Given two angles (let's say ∠A and ∠B) and the side (AB) between them.
- We can construct the triangle by drawing the side AB and then using the angles to find points A and B.
- Conclusion: Triangle construction is possible with this condition.
Final Answer:
The condition under which the construction of a triangle is NOT possible is Option A: Two sides and one angle (not included).
---
- Given two sides (let's say AB and AC) and an angle (∠A) that is not between them.
- In this case, we can draw the two sides AB and AC from point A, but we cannot determine where point C will lie because the angle is not included between the two sides.
- Therefore, we cannot complete the triangle construction as we do not know the position of point C.
- Conclusion: Triangle construction is not possible with this condition.
- Given two sides (let's say AB and AC) and the included angle (∠A).
- Here, we can construct the triangle by drawing side AB and then using the angle ∠A to determine the position of point C.
- Conclusion: Triangle construction is possible with this condition.
- Given three sides (let's say lengths a, b, and c).
- We can construct the triangle by drawing one side (say AB), and then using the lengths of the other two sides to find point C.
- Conclusion: Triangle construction is possible with this condition.
- Given two angles (let's say ∠A and ∠B) and the side (AB) between them.
- We can construct the triangle by drawing the side AB and then using the angles to find points A and B.
- Conclusion: Triangle construction is possible with this condition.
The condition under which the construction of a triangle is NOT possible is Option A: Two sides and one angle (not included).
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - CONSTRUCTIONSEXERCISE - Achievers Section (HOTS)5videos
CONSTRUCTIONS
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - CLASS 9 SAMPLE PAPER FINAL 4EXERCISE - MATHEMATICS10videos
CLASS 9 SAMPLE PAPER FINAL 4
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - COORDINATE GEOMETRY EXERCISE - ACHIEVERS SECTION (HOTS)2videos
COORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One or More
Which one of the following is correct in respect of a right-angled triangle ?
ASum of the two angles of a triangle is greater than the third angleBSum of the two angles of a triangle is less than the third angleCSum of the two angles of a triangle is equal to the third angleDNone of these - Question 2 - Select One
In which one of the following cases, the construction of a quadrilateral ABCD is not possible?
ABC = 4.5cm, AD = 5.5cm, CD = cm
AC = 5.5cm and BD = 7cmBAB = 6cm, BC = 9.5cm, <A=75∘, <B=150∘ and <C=140∘CAB = 3.5cm, <A=125∘,<B=80∘BC=5.5cm and CD = 5 cmDAB = 4cm, BC =6cm, AC = 8cm, AD = 5.5cm and DC = 5cm - Question 3 - Select One
In which one of the following cases, the construction of a quadrilateral ABCD is not possible?
ABC=4.5cm,AD=5.5cm,CD=5cm,AC=5.5cmandBD=7cmBAB=6cm,BC=9.5cm,∠A=75∘,∠B=150∘andC=140∘CAB=3.5cm,∠A=125∘,∠B=80∘,BC=5.5cmandCD=5cmDAB=4cm,BC=6cm,AC=8cm,AD=5,5cmandDC=5cm
Mark against the correct answer:
With the angles given below, in which case the construction of triangle is possible?View SolutionUnder which of the following conditions is the relation, ΔH=ΔE+PΔV valid for a system :-
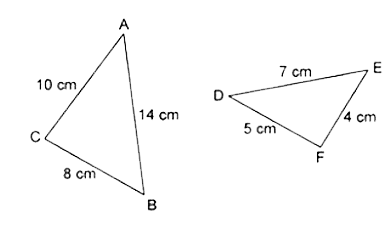
View SolutionWhich of [he following condition is TRUE about the similarity of triangle ABC and DEF given below?
View SolutionWe cannot construct a triangle, if we are given
View SolutionIn which of the following cases, a right triangle cannot be constructed ?
View Solution