Form the differential equation of the family of all the parabolas whose vertex is at origin and axis is y-axis.

A

$x \frac{d^{2} y}{{d x}^{2}} - \frac{d y}{d x} = 0$

B

$x \frac{d^{2} y}{{d x}^{2}} + \frac{d y}{d x} = 0$

C

$\frac{d^{2} y}{{d x}^{2}} - y = 0$

D

$\frac{d^{2} y}{{d x}^{2}} - \frac{d y}{d x} = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

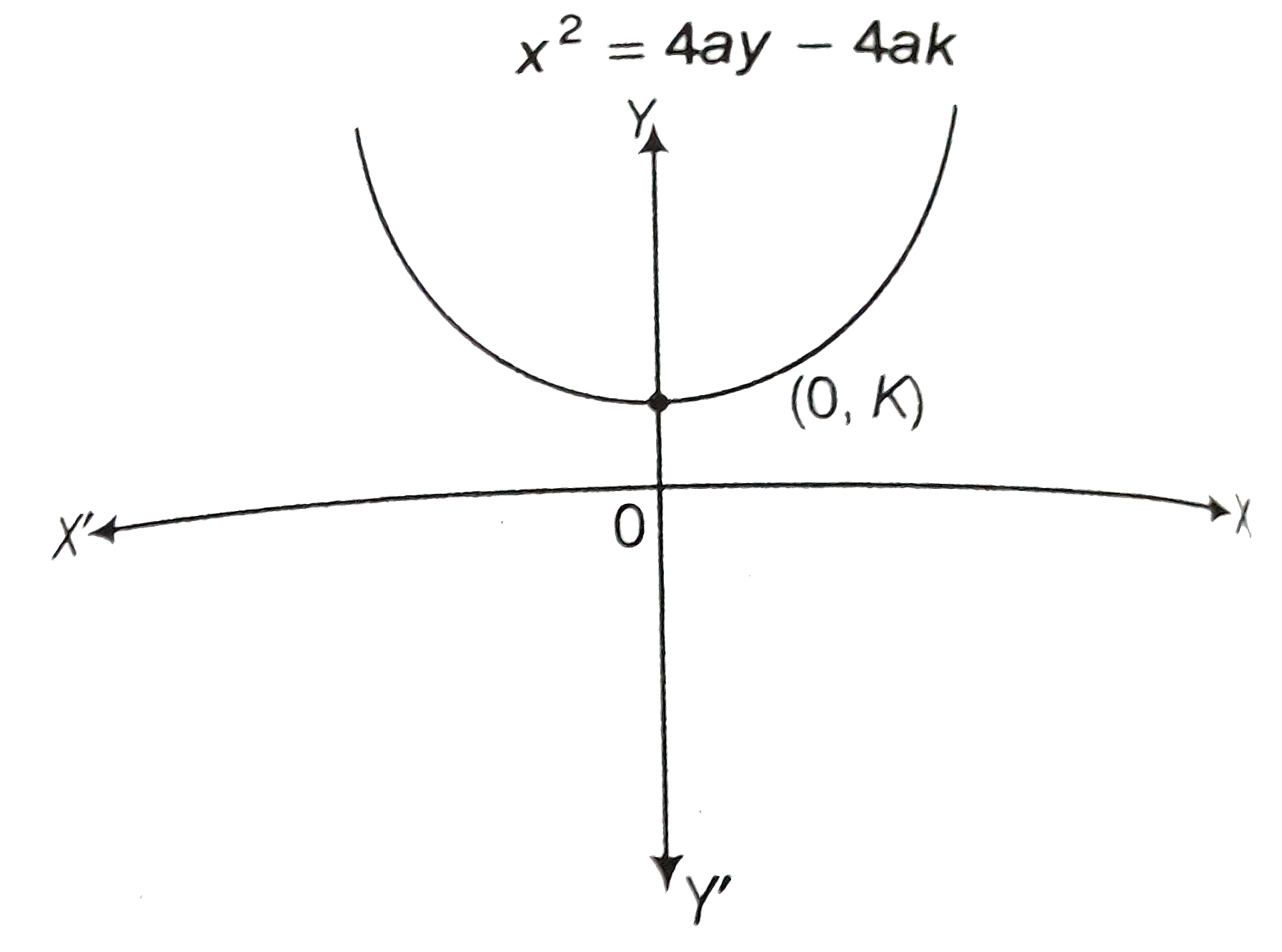
Axis of parabola=Y axis
and vertex of parabola is (0,k)
$∴$ Equation of parabola is
${(x - 0)}^{2} = 4 a (y - k)$
$x^{2} = 4 a y - 4 a k$

On differentiate both sides w.r.t. 'x', we get
$2 x = 4 a \frac{d y}{d x}$
$x = 2 a \frac{d y}{d x}$
$∴ \frac{1}{2 a} = \frac{1}{x} \frac{d y}{d x}$
On differentiatingg both sides w.r.tt. 'x', we get
$\frac{d}{d x} (\frac{1}{x} \cdot \frac{d y}{d x}) = \frac{d}{d x} (\frac{1}{2 a})$
$\Rightarrow \frac{1}{x} \cdot \frac{d^{2} y}{{d x}^{2}} + \frac{d y}{d x} (- \frac{1}{x^{2}}) = 0$
$∴ x \frac{d^{2} y}{{d x}^{2}} - \frac{d y}{d x} = 0$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The differential equation of the family of parabolas with focus at the origin and the X-axis as axis, is
A $y {(\frac{d y}{d x})}^{2} + 4 x \frac{d y}{d x} = 4 y$
B $- y {(\frac{d y}{d x})}^{2} = 2 x \frac{d y}{d x} - y$
C $y {(\frac{d y}{d x})}^{2} + y = 2 x y \frac{d y}{d x}$
D $y {(\frac{d y}{d x})}^{2} + 2 x y \frac{d y}{d x} + y = 0$
Question 2 - Select One
If m and n are respectively the order and degree of the differential equation of the family of parabolas with focus at the origin and X-axis as its axis , the mn-m + n=
A1
B4
C3
D2
Question 3 - Select One
The differential equation of the family of parabola with focus at the origin and the x-axis an axis, is
A $y {(\frac{d y}{d x})}^{2} + 4 x \frac{d y}{d x} = 4 y$
B $y {(\frac{d y}{d x})}^{2} = 2 x \frac{d y}{d x} - y$
C $y {(\frac{d y}{d x})}^{2} + y = 2 x y \frac{d y}{d x}$
D $y {(\frac{d y}{d x})}^{2} + 2 x y \frac{d y}{d x} + y - 0$

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-SOLVED PAPER 2017-MCQS

Home
Ask Doubt
Profile