From a set of $n (n > 1)$ numbers, all except one, which is $n - \frac{1}{4}$ are $n' s$ . Find the mean of all the $n$ numbers.

Video Solution

Text Solution

Verified by Experts

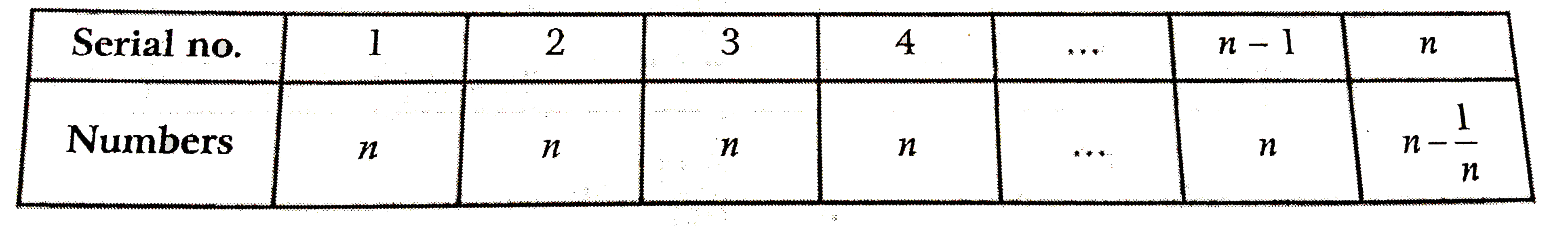
Let all numbers from 1 to $n$ are $n' s$ except the $n t h$ number, which is $n - \frac{1}{4}$ .
$S o, required mean = \frac{n + n + n + ... + n      (n - 1) times + (n - \frac{1}{n})}{n}$
$= \frac{n (n - 1) + (n - \frac{1}{n})}{n}$
$= \frac{n^{2} - \frac{1}{n}}{n} = n - \frac{1}{n^{2}}$

|

Updated on:21/07/2023

Class 9 MATHS STATISTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Given n numbers, $n > 1$ , of which,one is $1 - \frac{1}{n}$ and all others are 1's. The mean of the n numbers is
A $n - \frac{1}{n}$
B $1 - \frac{1}{n^{2}}$
C1
D $n - \frac{1}{n^{2}}$
Question 2 - Select One
Given n numbers, $n > 1$ , of which, one is $1 - \frac{1}{n}$ all others others are 1's . The mean of the n numbers is
A1
B $n - \frac{1}{n^{2}}$
C $n - \frac{1}{n}$
D $1 - \frac{1}{n^{2}}$
Question 3 - Select One
Let n(A) = n, then the number of all relations on A, is
A $2^{n}$
B $2^{n!}$
C $2^{n^{2}}$
DNone of these

NAGEEN PRAKASHAN-STATISTICS-Revision Exercise

Home
Ask Doubt
Profile