From a solid circular cylinder with height 12 cm and radius of the base 5 cm, a right circular cone of the same height and the same base radius is removed find the volume and total surface area of the remaing solid . [User π=3.14]
Radius of each of the cylinder and cone , r= 5 cm
Height of each of the cylinder and cone h= 12 cm
Slant height of the cone
l√r2+h2=√52+(12)2
=√169cm = 13 m
Volume of the remaining solid
volume of the cylinder - volume of the cone
πr2h−13πr2h=23πr2h
(23×3.14×5×5×12)cm3=628cm3
Total surface area of the reamining solid
= curved suface area of the cylinder + curved suface area of the cone + area of the upper circular face of the cylinder
2πrh+πrl+πr2=πr(2h+l+r)
=[3.14×5×(2×12+13+5)]cm2
=(3.14×5×42)cm2=659.cm2
(##RSA_MATH_X_C17_S01_018_S01.png" width="80%">
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREAS OF SOLIDSEXERCISE - VOLUME AND SURFACE AREA OF A COMBINATION OF SOLIDS (SOLVED EXAMPLES )2videos
VOLUME AND SURFACE AREAS OF SOLIDS
- BOOK - RS AGGARWALCHAPTER - VOLUME AND SURFACE AREAS OF SOLIDSEXERCISE - Exercise 17A28videos
VOLUME AND SURFACE AREAS OF SOLIDS
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES EXERCISE - Exercise 1215videos
TRIGONOMETRIC RATIOS OF COMPLEMENTARY ANGLES
Similar Questions
From a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the the same height and same base is removed . find the volume of the remaining solid
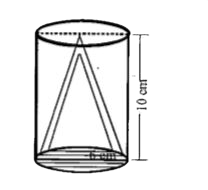 View Solution
View SolutionFrom a right circular cylinder with height 10cm and radius of base 6cm, a right circular cone of the same height and base is removed. Find the volume of the remaining solid.
View Solution
Knowledge Check
- Question 1 - Select One
From a solid cylinder of height 10 cm and radius of the base 6 cm, a cone of same height and same base is removed. The volume of the remaining solid is :
A240π cu. cmB5280 cu. cmC620π cu. cmD360π cu. cm - Question 2 - Select One
The volume of a right circular cone of height 12cm and base radius 6cm, is
A(12π)cm3B(36π)cm3C(72π)cm3D(144π)cm3
From a solid right circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and base is removed. Find the volume of the remaining solid. (Take π=3.14)
View SolutionFrom a solid circular cylinder with height 10 cm and radius of the base 6 cm, a circular cone of the same height and same base is removed. Find the volume of remaining solid and also find the whole surface area.
View SolutionFrom a solid cylinder whose height is 15 cm and diameter 16 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid. [Useπ=3.14.]
View SolutionFrom a circular cylinder of diameter 10 cm and height 12 cm a conical cavity of the same base radius and of the same height in hollowed out. Find the volume and the whole surfce of the remianing solid .Leave the answer in π.
View SolutionFrom a solid cylinder whose height is 8 cm and radius 6cm , a conical cavity of height 8 cm and of base radius 6 cm is hollowed out . Find the volume of the remaining solid.Also find the total surface area of the reamining solid.[ Take π=3.14 ]
View SolutionFind the curved surface area of a right circular cone whose slant height is 10cm and base radius is 7cm.
View Solution
