From a tap of inner radius 0.75cm, water flows at the rate of 7m per second. Find the volume in litres of water delivered by the pipe in one hour.
To solve the problem of finding the volume of water delivered by a tap in one hour, we can follow these steps:
Step 1: Identify the given values
- Inner radius of the tap (r) = 0.75 cm
- Speed of water flow (l) = 7 m/s = 700 cm/s (since 1 m = 100 cm)
Step 2: Calculate the cross-sectional area of the pipe
The formula for the area (A) of a circle is given by:
A=πr2
Substituting the value of r:
A=π(0.75)2
A=π(0.5625)
A≈1.7671cm2 (using π≈3.14)
Step 3: Calculate the volume of water flowing per second
The volume (V) of water flowing through the pipe per second can be calculated using the formula:
V=A×l
Substituting the values we have:
V=1.7671cm2×700cm/s
V≈1237.5cm3
Step 4: Calculate the volume of water delivered in one hour
Since there are 3600 seconds in one hour, the total volume delivered in one hour is:
Vhour=V×3600
Substituting the volume per second:
Vhour=1237.5cm3×3600
Vhour=4453500cm3
Step 5: Convert the volume from cubic centimeters to liters
Since 1 liter = 1000 cm³, we convert the volume:
Vliters=4453500cm31000
Vliters=4453.5liters
Final Answer
The volume of water delivered by the pipe in one hour is approximately 4453.5 liters.
---
- Inner radius of the tap (r) = 0.75 cm
- Speed of water flow (l) = 7 m/s = 700 cm/s (since 1 m = 100 cm)
The formula for the area (A) of a circle is given by:
A=πr2
Substituting the value of r:
A=π(0.75)2
A=π(0.5625)
A≈1.7671cm2 (using π≈3.14)
The volume (V) of water flowing through the pipe per second can be calculated using the formula:
V=A×l
Substituting the values we have:
V=1.7671cm2×700cm/s
V≈1237.5cm3
Since there are 3600 seconds in one hour, the total volume delivered in one hour is:
Vhour=V×3600
Substituting the volume per second:
Vhour=1237.5cm3×3600
Vhour=4453500cm3
Since 1 liter = 1000 cm³, we convert the volume:
Vliters=4453500cm31000
Vliters=4453.5liters
The volume of water delivered by the pipe in one hour is approximately 4453.5 liters.
Topper's Solved these Questions
Similar Questions
Water flows through a cylindrical pipe of internal diameter 7 cm at 5 metre per second. Calculate :
(i) the volume, in litres, of water discharged by the pipe in one minute,
(ii) the time, in minutes, the pipe would take to fill an empty rectangular tank 4m×3m×2.31m.
View SolutionWater is being pumped out through a circular pipe whose internal diameter is 7 cm. If the flow of water is 72 cm per second, how many litres of water are being pumped out in one hour?
View SolutionWater running in a cylindrical pipe of inner diameter 7 cm, is collected in a container at the rate of 192.5 litres per minute. Find the rate flow of water in the pipe in km/hr.
View SolutionThe given figure shows the cross-section of a water channel consisting of a rectangle and a semi-circle. Assuming that the channel is always full, find the
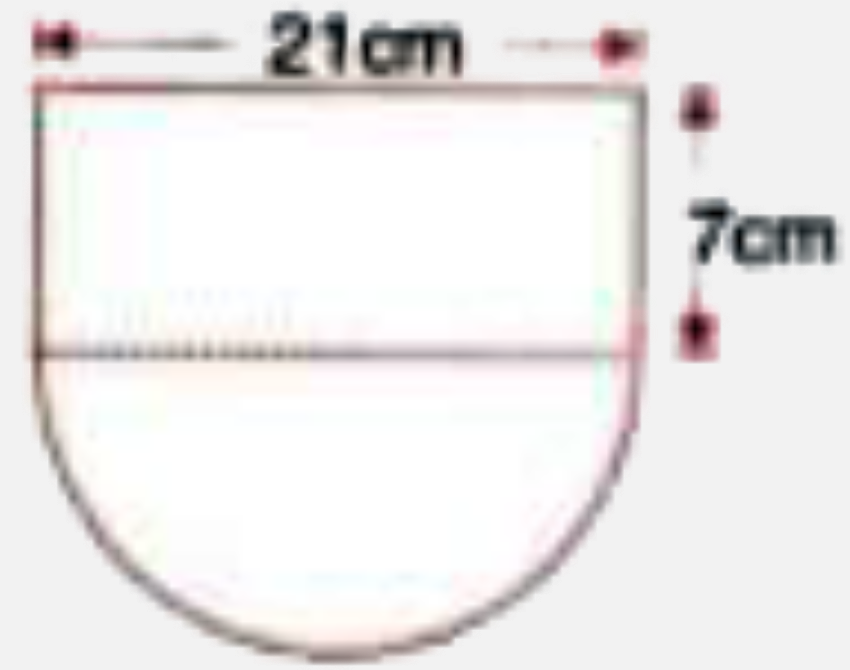
volume of water discharged through it in one minute if water is flowing at the rate of 20 cm per second. Give your answer in cubic metres correct to one place of decimal.
View SolutionThe volume of a sphere is increasing at the rate of 3 cubic centimeter per second. Find the rate of increase of its surface area, when the radius is 2 cm.
View SolutionThe volume of a sphere is increasing at the rate of 3 cubic centimeter per second. Find the rate of increase of its surface area, when the radius is 2 cm.
View SolutionThe volume of metal in a hollow sphere is constant. If the inner radius is increasing at the rate of 1 cm/sec, find the rate of increase of the outer radius when the radii are 4 cm and 8 cm respectively.
View SolutionWater flows out through a circular pipe whose internal diameter is 2cm, at the rate of 6 metres per second into a cylindrical tank. The radius of whose base is 60cm. Find the rise in the level of water in 30 minutes?
View SolutionWater flows out through a circular pipe whose internal diameter is 2cm, at the rate of 6 metres per second into a cylindrical tank. The water is collected in a cylindrical vessel radius of whose base is 60cm. Find the rise in the level of water in 30 minutes?
View SolutionWater flows out through a circular pipe whose internal diameter is 2cm, at the rate of 6 metres per second into a cylindrical tank. The water is collected in a cylindrical vessel radius of whose base is 60cm. Find the rise in the level of water in 30 minutes?
View Solution
