From the biconditional statement p↔q, where.
(i) p: The units digits of an interger is zero.
q: It is divisble by 5.
(ii) p: A Natural number is odd.
q: Natyral number n is not divisible by 2.
(iii) p: A triangle is an equalateral triangle .
q: All the three sides of a triangle are equal.
The correct Answer is:N/a
To solve the problem, we need to convert the given biconditional statements into conditional statements. A biconditional statement of the form p⟺q can be expressed as two conditional statements: p⟹q and q⟹p.
Let's break down each part of the question step by step.
(i)
Given:
- p: The unit digit of an integer is zero.
- q: It is divisible by 5.
Biconditional Statement:
p⟺q
Step 1: Write the conditional statements.
1. If the unit digit of an integer is zero, then it is divisible by 5.
- This is p⟹q.
2. If it is divisible by 5, then the unit digit of an integer is zero.
- This is q⟹p.
Final Conditional Statements:
- p⟹q: If the unit digit of an integer is zero, then it is divisible by 5.
- q⟹p: If it is divisible by 5, then the unit digit of an integer is zero.
(ii)
Given:
- p: A natural number is odd.
- q: A natural number n is not divisible by 2.
Biconditional Statement:
p⟺q
Step 1: Write the conditional statements.
1. If a natural number is odd, then it is not divisible by 2.
- This is p⟹q.
2. If a natural number is not divisible by 2, then it is odd.
- This is q⟹p.
Final Conditional Statements:
- p⟹q: If a natural number is odd, then it is not divisible by 2.
- q⟹p: If a natural number is not divisible by 2, then it is odd.
(iii)
Given:
- p: A triangle is an equilateral triangle.
- q: All three sides of a triangle are equal.
Biconditional Statement:
p⟺q
Step 1: Write the conditional statements.
1. If a triangle is an equilateral triangle, then all three sides of the triangle are equal.
- This is p⟹q.
2. If all three sides of a triangle are equal, then it is an equilateral triangle.
- This is q⟹p.
Final Conditional Statements:
- p⟹q: If a triangle is an equilateral triangle, then all three sides of the triangle are equal.
- q⟹p: If all three sides of a triangle are equal, then it is an equilateral triangle.
Summary of Conditional Statements:
1. For (i):
- p⟹q: If the unit digit of an integer is zero, then it is divisible by 5.
- q⟹p: If it is divisible by 5, then the unit digit of an integer is zero.
2. For (ii):
- p⟹q: If a natural number is odd, then it is not divisible by 2.
- q⟹p: If a natural number is not divisible by 2, then it is odd.
3. For (iii):
- p⟹q: If a triangle is an equilateral triangle, then all three sides of the triangle are equal.
- q⟹p: If all three sides of a triangle are equal, then it is an equilateral triangle.
Given:
- p: The unit digit of an integer is zero.
- q: It is divisible by 5.
p⟺q
1. If the unit digit of an integer is zero, then it is divisible by 5.
- This is p⟹q.
2. If it is divisible by 5, then the unit digit of an integer is zero.
- This is q⟹p.
- p⟹q: If the unit digit of an integer is zero, then it is divisible by 5.
- q⟹p: If it is divisible by 5, then the unit digit of an integer is zero.
Given:
- p: A natural number is odd.
- q: A natural number n is not divisible by 2.
p⟺q
1. If a natural number is odd, then it is not divisible by 2.
- This is p⟹q.
2. If a natural number is not divisible by 2, then it is odd.
- This is q⟹p.
- p⟹q: If a natural number is odd, then it is not divisible by 2.
- q⟹p: If a natural number is not divisible by 2, then it is odd.
Given:
- p: A triangle is an equilateral triangle.
- q: All three sides of a triangle are equal.
p⟺q
1. If a triangle is an equilateral triangle, then all three sides of the triangle are equal.
- This is p⟹q.
2. If all three sides of a triangle are equal, then it is an equilateral triangle.
- This is q⟹p.
- p⟹q: If a triangle is an equilateral triangle, then all three sides of the triangle are equal.
- q⟹p: If all three sides of a triangle are equal, then it is an equilateral triangle.
1. For (i):
- p⟹q: If the unit digit of an integer is zero, then it is divisible by 5.
- q⟹p: If it is divisible by 5, then the unit digit of an integer is zero.
2. For (ii):
- p⟹q: If a natural number is odd, then it is not divisible by 2.
- q⟹p: If a natural number is not divisible by 2, then it is odd.
- p⟹q: If a triangle is an equilateral triangle, then all three sides of the triangle are equal.
- q⟹p: If all three sides of a triangle are equal, then it is an equilateral triangle.
Topper's Solved these Questions
- MATHEMATICAL REASONING BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - MATHEMATICAL REASONING EXERCISE - OBJECTIVE TYPE QUESTIONS
21 Videos
- LINEAR INEQUALITIESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - LINEAR INEQUALITIESEXERCISE - Objective Type Questions
14 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Matching The Columns
5 Videos
Similar Questions
Knowledge Check
Which of the following must be true?
(I) The area of triangle P.
(II) The area of triangle Q.
(III) The area of triangle R.
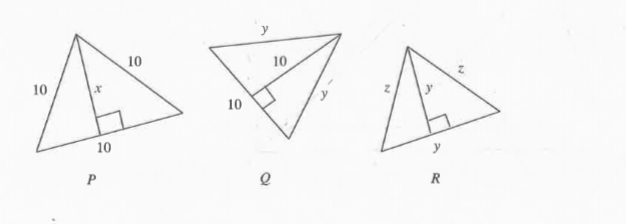 AI = II = IIIBI lt II lt IIICI gt II lt IIIDIII lt I lt II
AI = II = IIIBI lt II lt IIICI gt II lt IIIDIII lt I lt II
Write the contrapositive of the following statement
(i) If a quandrilateral is rectangle then it is a parallelogram
(ii) If a number is even , then it is divisble by 2
(iii) If end digit of a number is 0 , then it is divisble by 10
View SolutionWrite the converse of the following statement
(i) If a number n is odd , then n2 is odd
If a number is divisble by 6 , then it is divisble by both 2 and 3
(iii) If 3√a is an irrational number then a is not a perfect cube
View SolutionConsider a number N = 2 1 P 5 3 Q 4. The number of ordered pairs (P,Q) so that the number 'N' is divisible by 44, is
View SolutionConsider a number N=21 P 5 3 Q 4.
The number of ordered pairs (P,Q) so that the number' N' is divisible by 9, is
View SolutionGiven below are two pairs of statements. Combine these two statements using if and only if: p: if the sum of the digits of a number is divisible by 3, then the number is divisible by 3. q: if a number is divisible by 3, then the sum of its divisible by 3.
View SolutionPQRSTU is a regular hexagon. Determine each angle of triangle PQT .
View SolutionIs zero a rational number? Can it be written in the form pq, where p and q are integers and q≠0 ?
View Solution
