From the differential equation of the family of all parabolas having vertex at the origin and axis along the positive direction of the x-axis is given by
Video Solution
Text Solution
The general equation oof a parabola having vertex at the origin and axis along the positive direction of the x-axis is given by
y2=4ax …(i), where a is the parameter.
Since this equation contains one parameter, so we shall differentiate it only once to get the requisite differential equation.
Sifferentiating (i) w.e.t., we get
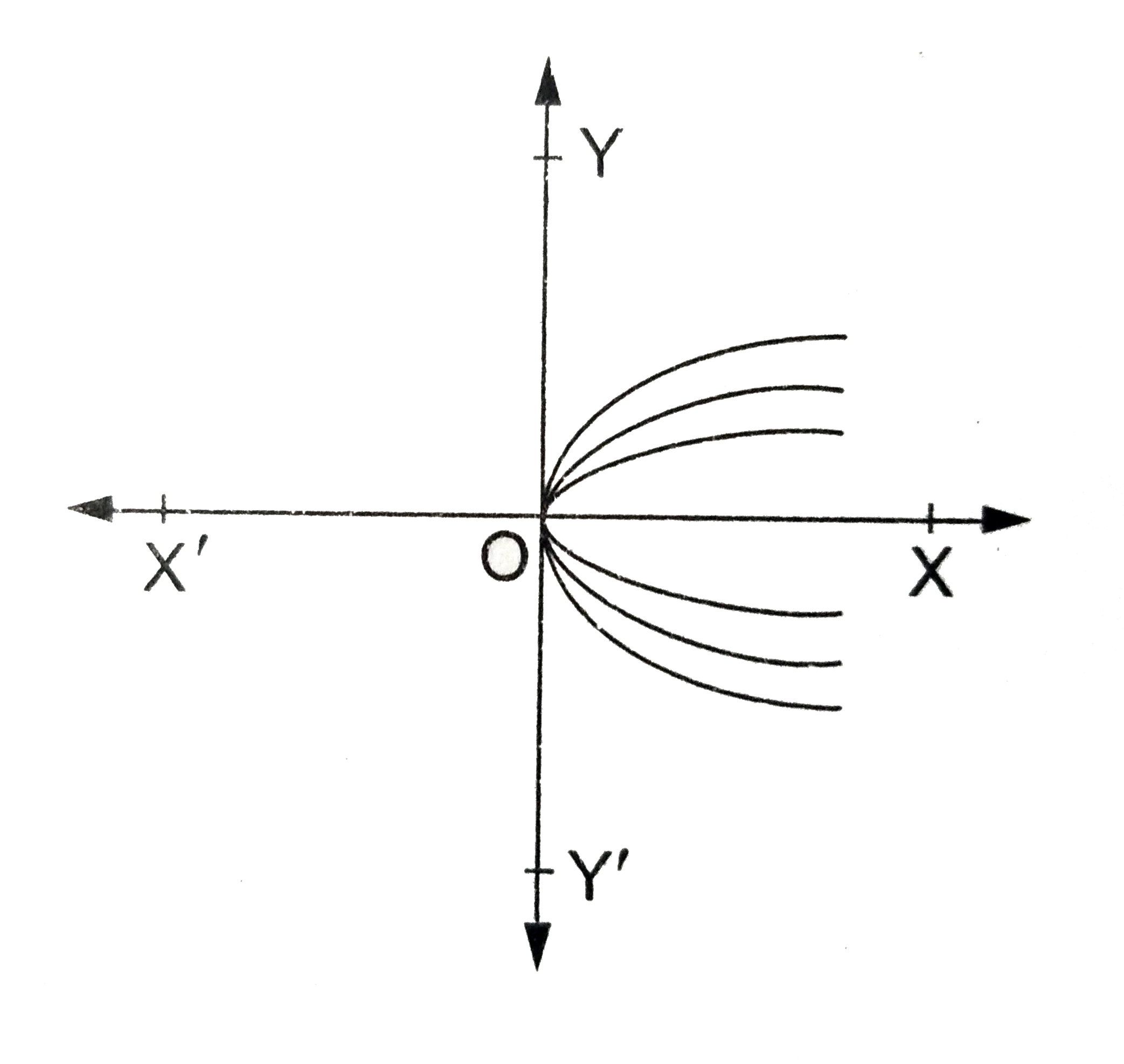
2ydydx=4n⇒ydydx=2a
⇒a=12ydydx. ...(ii)
Putting the value of a from (ii) in (i) we get
y2=4×12ydydx×ξmpliesy2−2xydydx=0.
Hence, y2−2xydydx=0 is the required differential equation.
|
Topper's Solved these Questions
- DIFFERENTIAL EQUATIONS AND THEIR FORMATION BOOK - RS AGGARWALCHAPTER - DIFFERENTIAL EQUATIONS AND THEIR FORMATION EXERCISE - Exercise 18A
18 Videos
- DIFFERENTIAL EQUATIONS AND THEIR FORMATION BOOK - RS AGGARWALCHAPTER - DIFFERENTIAL EQUATIONS AND THEIR FORMATION EXERCISE - Exercise 18B
17 Videos
- DETERMINANTSBOOK - RS AGGARWALCHAPTER - DETERMINANTSEXERCISE - Objective Questions
29 Videos
- DIFFERENTIAL EQUATIONS WITH VARIABLE SEPARABLEBOOK - RS AGGARWALCHAPTER - DIFFERENTIAL EQUATIONS WITH VARIABLE SEPARABLEEXERCISE - Exercise 19B
60 Videos
Similar Questions
Knowledge Check
The differential equation of the family of parabolas with focus at the origin and the X-axis as axis, is
Ay(dydx)2+4xdydx=4yB−y(dydx)2=2xdydx−yCy(dydx)2+y=2xydydxDy(dydx)2+2xydydx+y=0The differential equation of the family of parabola with focus at the origin and the x-axis an axis, is
Ay(dydx)2+4xdydx=4yBy(dydx)2=2xdydx−yCy(dydx)2+y=2xydydxDy(dydx)2+2xydydx+y−0What is the differential equation to family of parabola having their vertices at the origin and foci on the X-axis ?
Ay = 2x y'Bx = 2y y'Cxy = y'Dx = yy'
Form the differential equation representing the parabolas having vertex at the origin and axis along positive direction of x-axis.
View SolutionForm the differential equation of the family of all the parabolas whose vertex is at origin and axis is y-axis.
View SolutionThe order and degree of the differential equation of the family of parabolas having vertex at origin and axis along positive x-axis is
View SolutionForm the differential equation of the family of circles touching the x-axis at origin.
View SolutionForm the differential equation of the family of circles touching the y-axis at origin.
View Solution
