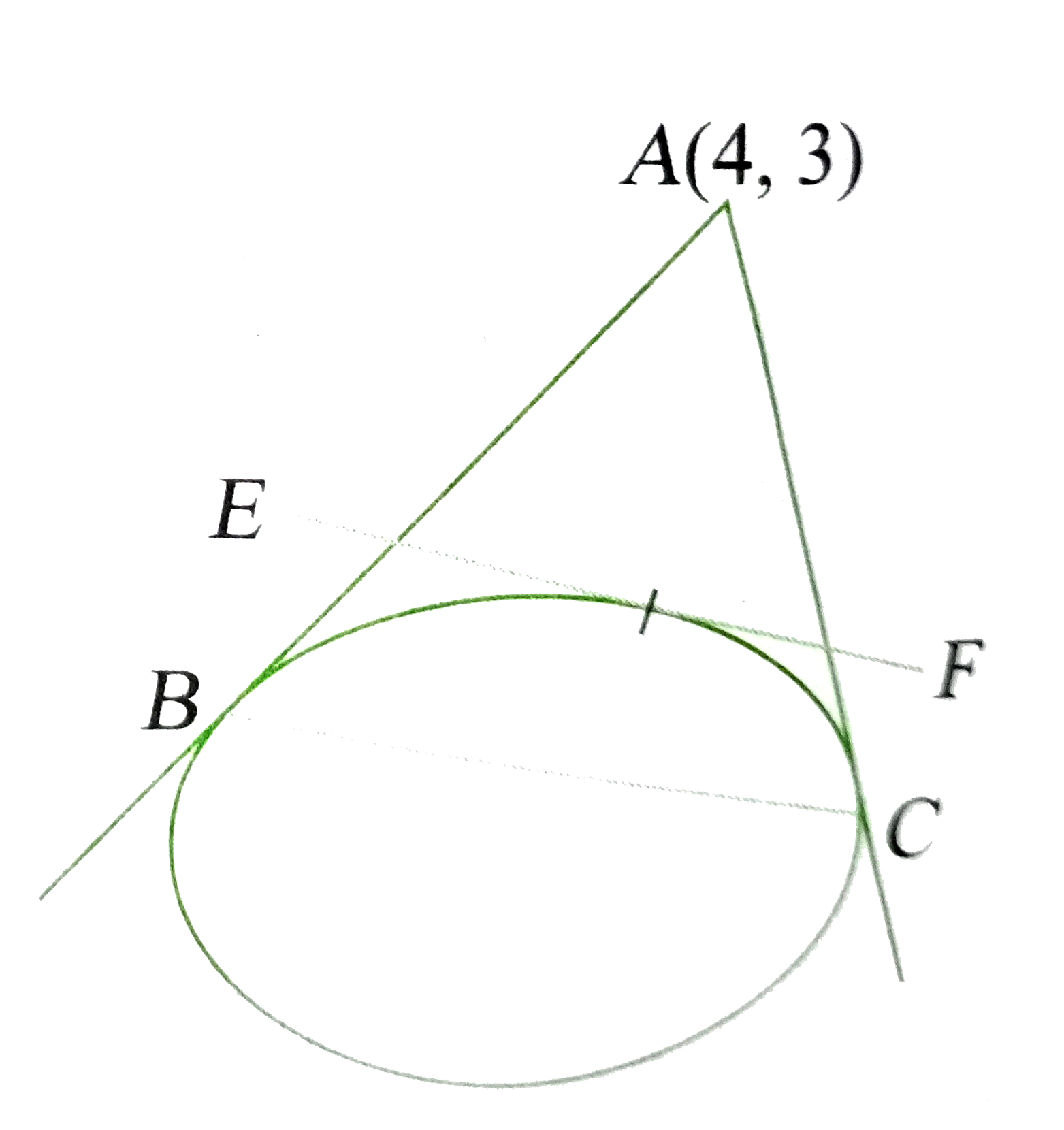
From the point $A (4, 3),$ tangent are drawn to the ellipse $\frac{x^{2}}{16} + \frac{y^{2}}{9} = 1$ to touch the ellipse at $B$ and $C . E F$ is a tangent to the ellipse parallel to line $B C$ and towards point $A .$ Then find the distance of $A$ from $E F .$

Text Solution

Verified by Experts

The correct Answer is: $∣ ∣ 24 - 4 \sqrt{18} ∣ ∣ / 5$

Updated on:21/07/2023

Tangents are drawn from the point $P (3, 4)$ to the ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ touching the ellipse at points A and B. The orthocenter of the $△ P A B$ is
A $(5, \frac{8}{7})$
B $(\frac{7}{5}, \frac{25}{8})$
C $(\frac{11}{5}, \frac{8}{5})$
D $(\frac{8}{25}, \frac{7}{5})$
Tangents are drawn from the point P(3,4) to the ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ touching the ellipse at point A and B. Q. The orthocenter of the trianlge PAB is
A $(5, \frac{8}{7})$
B $(\frac{7}{5}, \frac{25}{8})$
C $(\frac{11}{5}, \frac{8}{5})$
D $(\frac{8}{25}, \frac{7}{5})$
Tangents are drawn from the point P(3,4) to the ellipse $\frac{x^{2}}{9} + \frac{y^{2}}{4} = 1$ touching the ellipse at point A and B. Q. The coordinates of A and B are
A(3,0) amd (0,2)
B $(- \frac{8}{5}, (2 \frac{\sqrt{161}}{15}) and (- \frac{9}{8}, \frac{8}{5})$
C $(- \frac{8}{5}, (2 \frac{\sqrt{161}}{15}) and (0, 2)$
D $(3, 0) and (- \frac{9}{5}, \frac{8}{5})$