Question

$f\left(x\right)=|ax-b|+c\left|x\right|\forall x\in (-\infty ,\infty ),$
where $a>0,b>0,c>0.$
Find the condition if $f\left(x\right)$
attains the minimum value only at one point.

Explanation

`" "f(x)= {{:(b-ax-cx",",,xlt0), (b-ax+cx",",,0le x lt(b)/(a)), (ax-b+cx",",,x ge (b)/(a)):}`
`" "={{:(b-(a+c)x",",,xlt0), (b+(c-a)x",",,0lexlt(b)/(a)),((a+c)x-b",",,xge(b)/(a)):}`
The graphs of the function for different situations are as shown in the following figures.

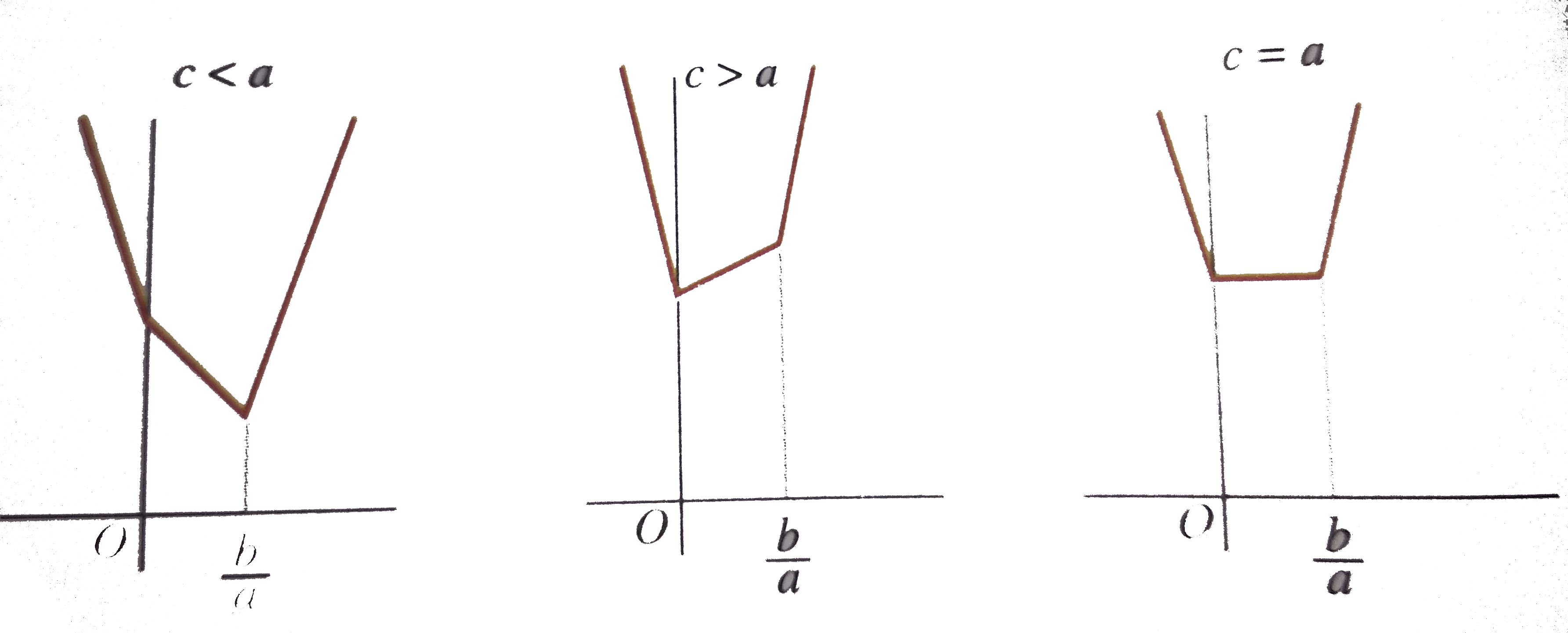
From the figure, we can see that for `c lt a and c gt a`, there is only point of minima.
For `c=a`, there are infinite points of minima.
Thus, for exactly one point of minima, `c ne a`.