Give reason to show that none of the numbers 640, 81000 and 3600000 is a perfect square.
To determine whether the numbers 640, 81000, and 3600000 are perfect squares, we can analyze their prime factorization and the properties of perfect squares.
Step 1: Prime Factorization
We will first find the prime factorization of each number.
1. For 640:
- Divide by 2: 640÷2=320
- Divide by 2: 320÷2=160
- Divide by 2: 160÷2=80
- Divide by 2: 80÷2=40
- Divide by 2: 40÷2=20
- Divide by 2: 20÷2=10
- Divide by 2: 10÷2=5
- Finally, 5 is a prime number.
Thus, the prime factorization of 640 is:
640=27×51
2. For 81000:
- Divide by 10: 81000÷10=8100
- Divide by 10: 8100÷10=810
- Divide by 10: 810÷10=81
- Now, factor 81: 81=34
Thus, the prime factorization of 81000 is:
81000=23×34×53
3. For 3600000:
- Divide by 100: 3600000÷100=36000
- Divide by 100: 36000÷100=360
- Now, factor 360: 360=36×10=62×10=(2×3)2×(2×5)=23×32×51
Thus, the prime factorization of 3600000 is:
3600000=26×32×54
Step 2: Check for Perfect Square
A number is a perfect square if all the exponents in its prime factorization are even.
1. For 640:
- Exponents: 7 (for 2), 1 (for 5)
- Since both exponents are odd, 640 is not a perfect square.
2. For 81000:
- Exponents: 3 (for 2), 4 (for 3), 3 (for 5)
- Since 2 and 5 have odd exponents, 81000 is not a perfect square.
3. For 3600000:
- Exponents: 6 (for 2), 2 (for 3), 4 (for 5)
- Since all exponents are even, 3600000 is a perfect square.
Conclusion
- 640 is not a perfect square because it has odd exponents in its prime factorization.
- 81000 is not a perfect square because it has odd exponents in its prime factorization.
- 3600000 is a perfect square because all exponents in its prime factorization are even.
We will first find the prime factorization of each number.
- Divide by 2: 640÷2=320
- Divide by 2: 320÷2=160
- Divide by 2: 160÷2=80
- Divide by 2: 80÷2=40
- Divide by 2: 40÷2=20
- Divide by 2: 20÷2=10
- Divide by 2: 10÷2=5
- Finally, 5 is a prime number.
640=27×51
- Divide by 10: 81000÷10=8100
- Divide by 10: 8100÷10=810
- Divide by 10: 810÷10=81
- Now, factor 81: 81=34
81000=23×34×53
- Divide by 100: 3600000÷100=36000
- Divide by 100: 36000÷100=360
- Now, factor 360: 360=36×10=62×10=(2×3)2×(2×5)=23×32×51
3600000=26×32×54
A number is a perfect square if all the exponents in its prime factorization are even.
- Exponents: 7 (for 2), 1 (for 5)
- Since both exponents are odd, 640 is not a perfect square.
- Exponents: 3 (for 2), 4 (for 3), 3 (for 5)
- Since 2 and 5 have odd exponents, 81000 is not a perfect square.
- Exponents: 6 (for 2), 2 (for 3), 4 (for 5)
- Since all exponents are even, 3600000 is a perfect square.
- 640 is not a perfect square because it has odd exponents in its prime factorization.
- 81000 is not a perfect square because it has odd exponents in its prime factorization.
- 3600000 is a perfect square because all exponents in its prime factorization are even.
Topper's Solved these Questions
- SQUARES AND SQUARE ROOTSBOOK - ICSECHAPTER - SQUARES AND SQUARE ROOTSEXERCISE - Exercise3 (B)
27 Videos
- SPECIAL TYPES OF QUADRILATERALSBOOK - ICSECHAPTER - SPECIAL TYPES OF QUADRILATERALSEXERCISE - EXERCISE
22 Videos
- SURFACE AREA, VOLUME AND CAPACITY. BOOK - ICSECHAPTER - SURFACE AREA, VOLUME AND CAPACITY. EXERCISE - EXERCISE ( E )
11 Videos
Similar Questions
Give reason to show that none of the numbers, given below, is a perfect square.
(i) 2162
(ii) 6843
(iii) 9637
(iv) 6598
View SolutionShow that 17640 is not a perfect square.
View SolutionFind the least number of six digits which is a perfect square.
View SolutionFind the greatest number of 5 digits which is a perfect square.
View SolutionFind the greatest number of 4 digits which is a perfect square.
View SolutionFind the least number of four digits which is a perfect square.
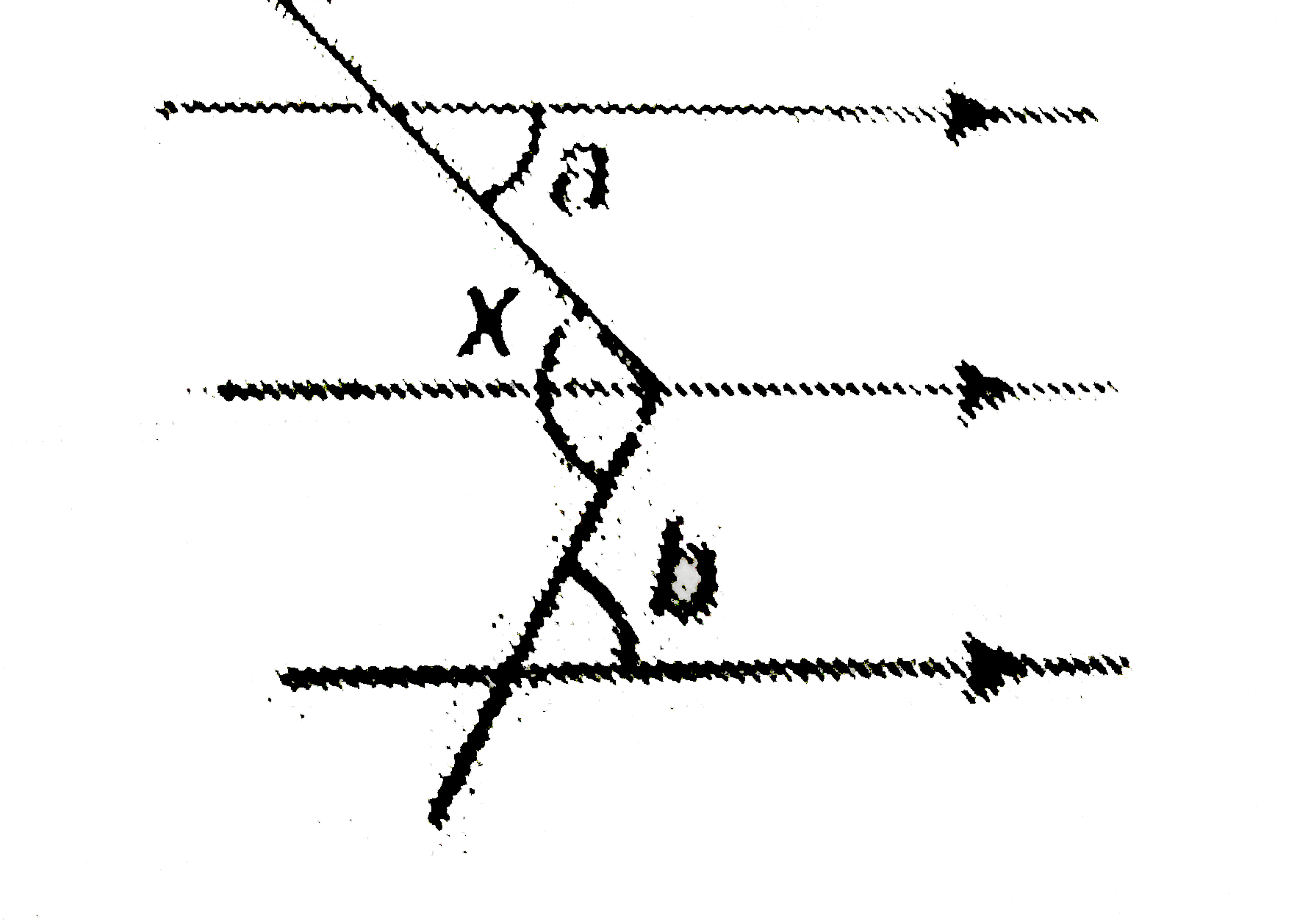
View SolutionGiving reason show that
∠x=∠a+∠b
View SolutionFind the least number of 4 digits which is a perfect square.
View SolutionFind the greatest number of two digits which is a perfect square.
View SolutionFind the greatest number of six digits which is a perfect square.
View Solution
