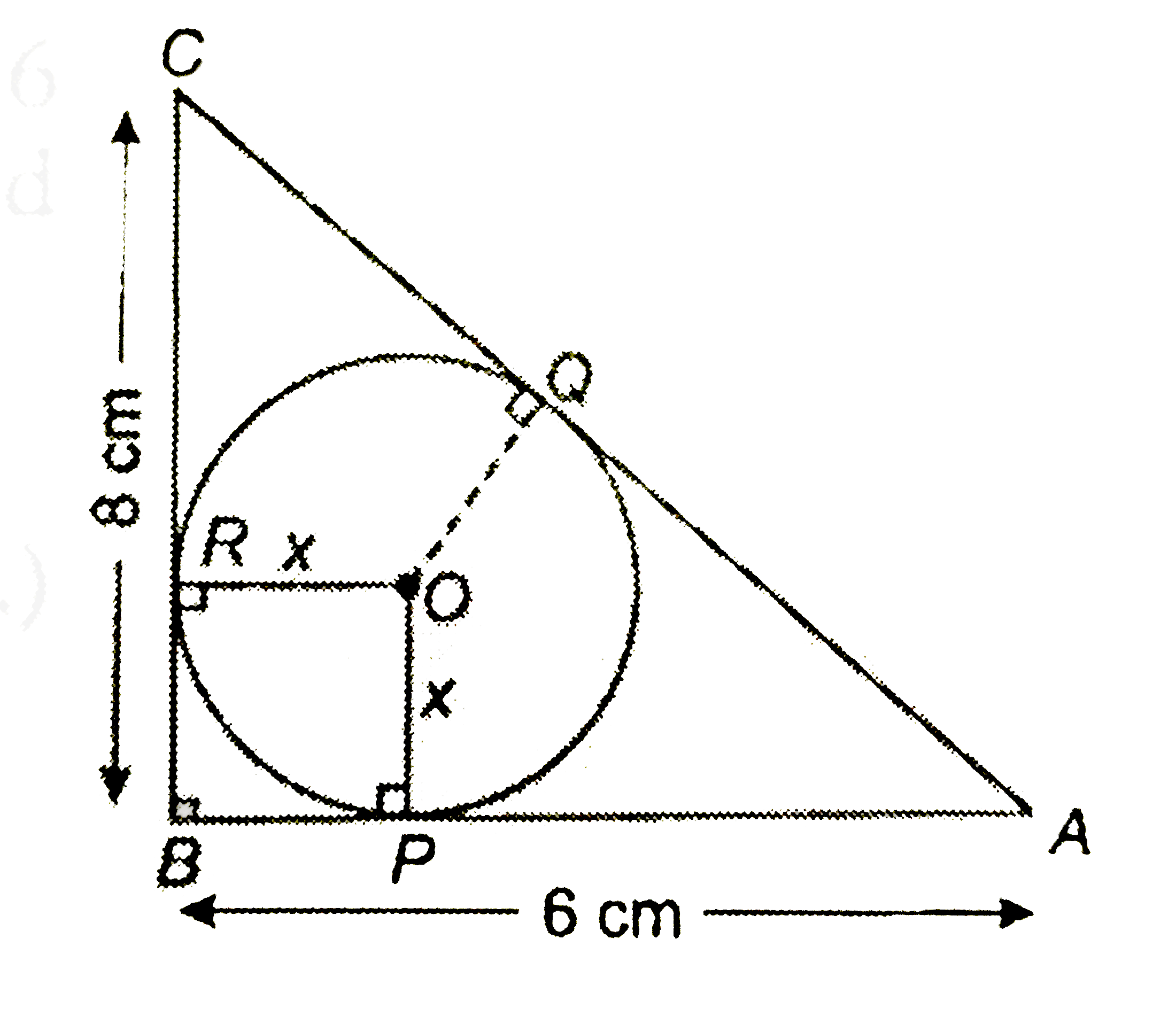
Given a right-angled . The lengths of the sides containing the right angle are 6 cm and 8 cm. A circle is inscribed in . Find the radius of the circle.
In ,we have
.
A circle is inscribed in . Let O be its centre and M,N and P be the points where it touches the sides AB,BC and CA respectively. Then,
.
Let r cm be the radius of the circle.
Then,
Now, [ by Pythagora's theorem]
.
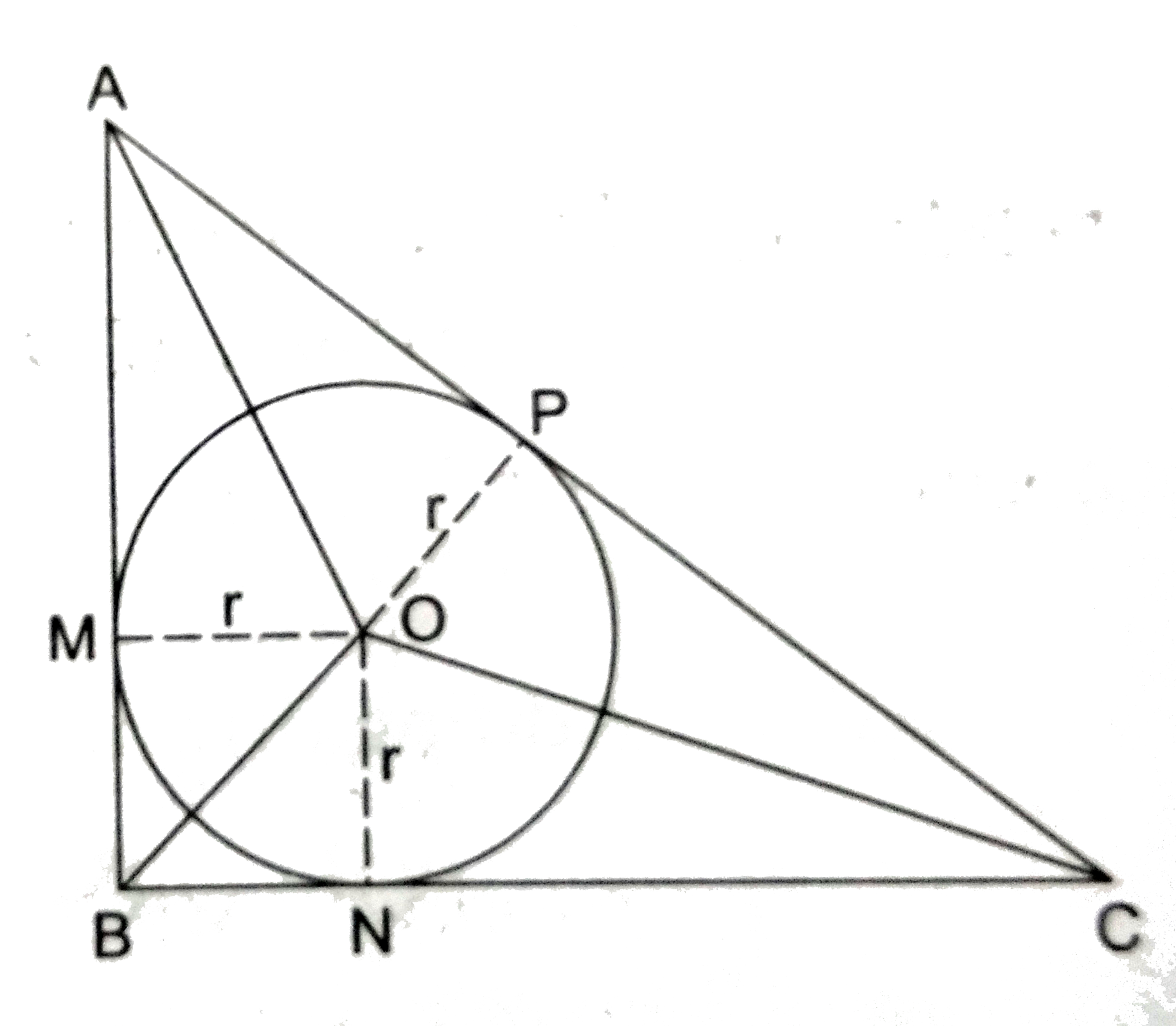
Now,
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Given a right angled △ABC. The lengths of the sides containing the right angle are 6 cm and 8 cm. A circule is inscribed in △ABC. Find th radius of the circle.
View SolutionIn triangle ABC,right angled at B, BC = 24 cm, and AB = 7 cm. A circle is inscribed in triangle ABC. Then the radius of the circle is:
View Solution
Knowledge Check
ABC is a right angle triangle right angled at A. A circle is inscribed in it the length of the two sidescontaining right angle are 6 cm and 8 cm then the radius of the circle is
A3 cmB2 cmC5 cmD4 cmABC is a right angled triangle, right at A, A circle is inscribed in it. The lengths of two sides containing the right angle are 48 cm and 14 cm . The radius of the inscribed circle is :
A)4 cm
B)8 cm
C)6 cm
D)5 cmA4 cmB8 cmC6 cmD5 cmThe base of a prism is a righ angle triangle and the two sides containing the right angle are 8 cm and 15 cm. If its heights is 20 cm, then the volume of the prism is :
A1600 ccB300 ccC1200 ccD600 cc
PQR is a right angled triangle at Q with QR =12 a=cm and PQ=5cm. A circle with centre O is inscribed in △PQR. Find the radius of the circle.
View SolutionAn equilateral triangle of side 9 cm is inscribed in a circle. Find the radius of the circle.
View SolutionAn equilateral triangle of side 9 cm is inscribed in a circle. Find the radius of the circle.
View SolutionABC is a right angle triangle right angled at A. A circle is inscribed in it the length of the two sidescontaining right angle are 6 cm and 8 cm then the radius of the circle is
View SolutionIn the given figure ABC is a right angled triangle with AB=6 cm, and BC=8 cm. A circle with centre O has been inscribed inside the triangle. Find the radius of the circle.
View Solution
