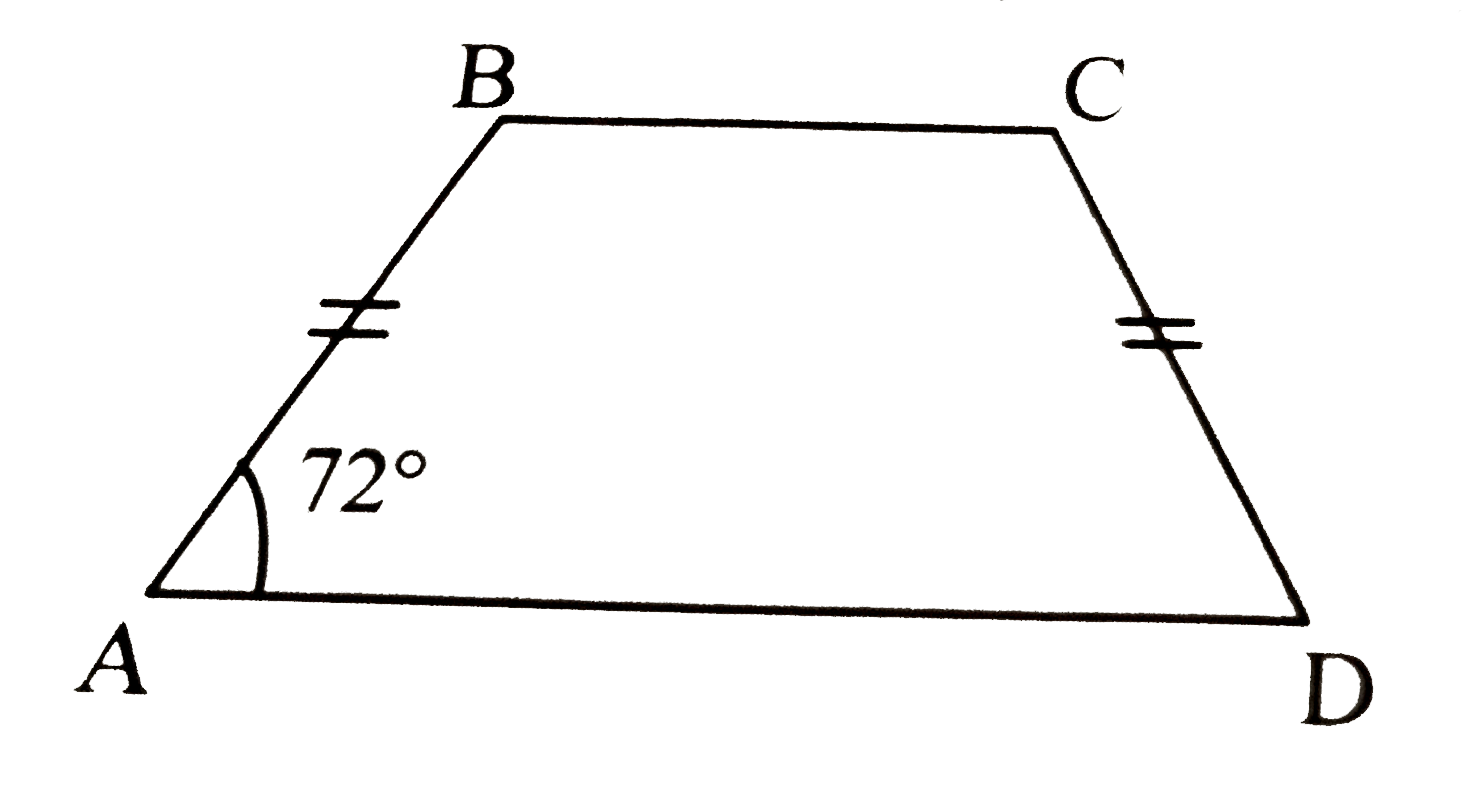
Given a trapezium ABCD in which AB||CD and AD = BC. If ∠C=76∘, then ∠D equals
14∘
104∘
76∘
none of these
The correct Answer is:C
To find the measure of angle D in trapezium ABCD where AB || CD and AD = BC, follow these steps:
Step 1: Understand the properties of trapezium
In trapezium ABCD, since AB is parallel to CD (AB || CD), we can use the properties of angles formed by parallel lines.
Hint: Remember that when two parallel lines are cut by a transversal, the alternate interior angles are equal.
Step 2: Identify given information
We are given that angle C = 76° and AD = BC, which indicates that trapezium ABCD is an isosceles trapezium.
Hint: An isosceles trapezium has non-parallel sides that are equal in length.
Step 3: Draw perpendiculars from points A and B to line CD
Drop perpendiculars from points A and B to line CD. Let these perpendiculars meet CD at points M and N respectively. This creates two right triangles: triangle ADM and triangle BNC.
Hint: Visualizing the trapezium with perpendiculars helps in analyzing the triangles formed.
Step 4: Analyze triangles ADM and BNC
In triangles ADM and BNC:
- Angle AMD = 90° (perpendicular from A)
- Angle BNC = 90° (perpendicular from B)
- AD = BC (given)
Hint: Use the properties of congruent triangles to find relationships between angles.
Step 5: Apply the congruence criteria
Since both triangles ADM and BNC have:
- Right angles (90°)
- One pair of equal sides (AD = BC)
- The distance between the parallel lines (AM = BN)
We can conclude that triangles ADM and BNC are congruent by the Hypotenuse-Leg (HL) theorem.
Hint: Congruent triangles have equal corresponding angles.
Step 6: Conclude that angle D equals angle C
Since triangles ADM and BNC are congruent, we have:
- Angle D = Angle C
Given that angle C = 76°, it follows that:
- Angle D = 76°
Hint: Use the property of corresponding parts of congruent triangles (CPCT).
Final Answer:
Thus, angle D equals 76°.
---
In trapezium ABCD, since AB is parallel to CD (AB || CD), we can use the properties of angles formed by parallel lines.
We are given that angle C = 76° and AD = BC, which indicates that trapezium ABCD is an isosceles trapezium.
Drop perpendiculars from points A and B to line CD. Let these perpendiculars meet CD at points M and N respectively. This creates two right triangles: triangle ADM and triangle BNC.
In triangles ADM and BNC:
- Angle AMD = 90° (perpendicular from A)
- Angle BNC = 90° (perpendicular from B)
- AD = BC (given)
Since both triangles ADM and BNC have:
- Right angles (90°)
- One pair of equal sides (AD = BC)
- The distance between the parallel lines (AM = BN)
Since triangles ADM and BNC are congruent, we have:
- Angle D = Angle C
- Angle D = 76°
Thus, angle D equals 76°.
Topper's Solved these Questions
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - POLYGONS AND QUADRILATERALS EXERCISE - QUESTION BANK - 2320videos
POLYGONS AND QUADRILATERALS
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PERCENTAGE AND ITS APPLICATIONSEXERCISE - SELFT ASSESMENT SHEET (SECTION-C DISCOUNT )10videos
PERCENTAGE AND ITS APPLICATIONS
- BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - PROBABILITYEXERCISE - SELF ASSESSMENT SHEET -2910videos
PROBABILITY
Similar Questions
Knowledge Check
- Question 1 - Select One
In a trapezium ABCD, AB||DC, AB = AD, ∠ADC=64∘and∠BCD=54∘. Find ∠DBC.
 A64∘B72∘C94∘D116∘
A64∘B72∘C94∘D116∘ - Question 2 - Select One
ABCD is an isosceles trapezium in which ¯¯¯¯¯¯AB||¯¯¯¯¯¯CDand∠A=57∘ . Find the value of ∠C+∠D.
A112∘B123∘C246∘D303∘ - Question 3 - Select One
ABCD is a cyclic trapezium such that AD || BC. If ∠ABC=70∘, then the value of ∠BCD is :
A60∘B70∘C40∘D80∘
ABCD is a trapezium in which AB||CD and AD=BC (see figure). Show that
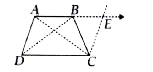
∠A=∠BView SolutionABCD is a trapezium in which AB∣∣DC ∠A=∠B=30degree. Find ∠C and ∠D. Are these angles equal?
 View Solution
View SolutionABCD is a kite in which AB=AD and CB=CD. If ∠ABD=25∘and∠BDC=35∘, then find ∠A−∠C.
View SolutionABCD is a kite in which AB=AD and CB=CD. If ∠ABD=30∘and∠BDC=40∘, then find ∠A+∠C.
View SolutionIn trapezium ABCD with AB||CD, if ∠A=100°, then ∠D= __________.
View Solution