Given an arc of a circle, complete the circle.
Let
PQ be an arc of the circle.
In Order to complete the circle we have to find its Center and radius
Take a point R on the are
PQ and joinPR and QR
Draw perpendicular bisector of PR and RQ respectively
Let these perpendicular Bisector intersect bisector at point O
Then , OP=OQ
Draw a circle with centre O and radius=OP=OQ to get the required circle
Similar Questions
. Prove that the tangent drawn at the mid-point of an arc of a circle is parallel to the chord joining the end points of the arc.
View SolutionIf the locus of the complex number z given by arg(z+i)−arg(z−i)=2π3 is an arc of a circle, then the length of the arc is
View SolutionThe locus of the centre of a circle the touches the given circle externally is a _______
View SolutionThe radius of a circle is 50 cm. Find the angle subtends by an arc of 22 cm length at the centerof the circle.
View SolutionAn arc 15 ft long describes an angle of 5 radians at the centre of a circle. Find the radius of the circle.
View SolutionAn arc of length 20π cm subtends an angle of 144o at the centre of a circle. Find the radius of the circle.
View Solution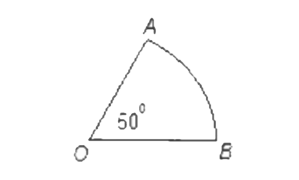
In the figure abvoe, aB is the arc of a circle with centre O. If the length of arc AB is 4π, what is the area of region OAB to the nearest tenth?
View SolutionProve that the right bisector of a chord of a circle, bisects the corresponding arc or the circle.
View SolutionProve that the right bisector of a chord of a circle, bisects the corresponding arc or the circle.
View SolutionIf two arcs of a circle (or of congruent circles) are congruent, then corresponding chords are equal.
View Solution
