Given are the lengths of three sides of a triangle in centimeters. Which of the following triplets can form a right-angled triangle ?
The correct Answer is:a. and d.
To determine which of the given triplets can form a right-angled triangle, we will use the Pythagorean theorem. According to this theorem, in a right-angled triangle, the square of the length of the hypotenuse (the longest side) is equal to the sum of the squares of the lengths of the other two sides.
1. Identify the Triplets: We have three sets of lengths given. Let's denote them as:
- Triplet 1: 15 cm, 14 cm, 7 cm
- Triplet 2: 40 cm, 41 cm, 12 cm
- Triplet 3: 8 cm, 15 cm, 17 cm
2. Apply the Pythagorean Theorem: For each triplet, we will check if the sum of the squares of the two smaller sides equals the square of the longest side.
3. Check Triplet 1 (15, 14, 7):
- Identify the longest side: 15 cm
- Calculate:
- 142+72=196+49=245
- 152=225
- Compare: 245≠225
- Conclusion: This triplet does not form a right-angled triangle.
4. Check Triplet 2 (40, 41, 12):
- Identify the longest side: 41 cm
- Calculate:
- 402+122=1600+144=1744
- 412=1681
- Compare: 1744≠1681
- Conclusion: This triplet does not form a right-angled triangle.
5. Check Triplet 3 (8, 15, 17):
- Identify the longest side: 17 cm
- Calculate:
- 82+152=64+225=289
- 172=289
- Compare: 289=289
- Conclusion: This triplet forms a right-angled triangle.
Final Answer:
The triplet that can form a right-angled triangle is 8 cm, 15 cm, and 17 cm.
- Triplet 1: 15 cm, 14 cm, 7 cm
- Triplet 2: 40 cm, 41 cm, 12 cm
- Triplet 3: 8 cm, 15 cm, 17 cm
- Identify the longest side: 15 cm
- Calculate:
- 142+72=196+49=245
- 152=225
- Compare: 245≠225
- Conclusion: This triplet does not form a right-angled triangle.
- Identify the longest side: 41 cm
- Calculate:
- 402+122=1600+144=1744
- 412=1681
- Compare: 1744≠1681
- Conclusion: This triplet does not form a right-angled triangle.
- Identify the longest side: 17 cm
- Calculate:
- 82+152=64+225=289
- 172=289
- Compare: 289=289
- Conclusion: This triplet forms a right-angled triangle.
The triplet that can form a right-angled triangle is 8 cm, 15 cm, and 17 cm.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - CHALLENGE1videos
THE TRIANGLE AND ITS PROPERTIES
- BOOK - ICSECHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - REVISIONS EXERCISE15videos
THE TRIANGLE AND ITS PROPERTIES
- BOOK - ICSECHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 12.211videos
THE TRIANGLE AND ITS PROPERTIES
- BOOK - ICSECHAPTER - SYMMETRYEXERCISE - Exercise 19B13videos
SYMMETRY
- BOOK - ICSECHAPTER - UNITARY METHODEXERCISE - EXERCISE16videos
UNITARY METHOD
Similar Questions
Knowledge Check
- Question 1 - Select One
A triangle with side lengths of 5, 12, and 15 centimeters is similar to another triangle. The longest side of the other triangle has length 24 centimeters. What is the perimeter, in centimeters, of the triangle?
A38.4B44C51.2D58
Find the length of side BC in the given triangle.
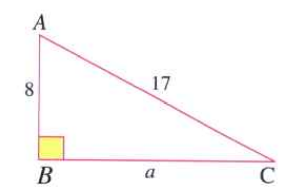 View Solution
View SolutionIf the sides of a triangle are in the ratio 1:√2:1, show that it is a right-angled triangle.
View SolutionIf the sides of a triangle are 3 cm, 4 cm and 6 cm long, determine whether the triangle is right-angled triangle.
View SolutionIf the length of sides of right angled triangle are in AP, then their ratio is
View SolutionIf the lengths of the sides of a triangle are decided by the three thrown of a single fair die,then the probability that the triangle is of maximum area given that it is an isosceles triangle, is
View SolutionState true or false.
(a) The altitude of an acute-angled triangle lies outside the triangle.
(b) the orthocentre of an obtuse-angled triangle lies outside the triangle.
(c) the orthocentre is the point of concurrency of three medians of a triangle.
(d) The vertex containing the right angle is also the orthocentre of a right-angled triangle.View SolutionThe sides of a triangle are 5 cm, 8 cm and 11 cm respectively. Demtermine whether it is a right angled triangle or not.
View Solution
