Given n students in the class like football, what may 2n show? What may show? (Hint : Think of games other than football).
To solve the question, we need to analyze what the expressions 2n and n2 represent in the context of students who like football.
1. Understanding the given information:
- We know that there are n students in the class who like football.
2. Interpreting 2n:
- The expression 2n can be interpreted as twice the number of students who like football.
- Since n students like football, 2n could represent the total number of students who like another game (not football).
- Therefore, we can say that 2n students like another game, such as basketball or cricket.
3. Interpreting n2:
- The expression n2 represents half the number of students who like football.
- This could indicate that n2 students like a different game (again, not football).
- Thus, we can conclude that n2 students like another game, such as tennis or badminton.
Final Answers:
- 2n may show that there are 2n students who like another game (other than football).
- n2 may show that there are n2 students who like another game (other than football).
- We know that there are n students in the class who like football.
- The expression 2n can be interpreted as twice the number of students who like football.
- Since n students like football, 2n could represent the total number of students who like another game (not football).
- Therefore, we can say that 2n students like another game, such as basketball or cricket.
- The expression n2 represents half the number of students who like football.
- This could indicate that n2 students like a different game (again, not football).
- Thus, we can conclude that n2 students like another game, such as tennis or badminton.
- 2n may show that there are 2n students who like another game (other than football).
- n2 may show that there are n2 students who like another game (other than football).
Topper's Solved these Questions
- ALGEBRABOOK - MTG IIT JEE FOUNDATIONCHAPTER - ALGEBRAEXERCISE - NCERT SECTION (EXERCISE - 11.5)
30 Videos
- ALGEBRABOOK - MTG IIT JEE FOUNDATIONCHAPTER - ALGEBRAEXERCISE - EXERCISE (MULTIPLE CHOICE QUESTIONS) (LEVEL - I)
35 Videos
- ALGEBRABOOK - MTG IIT JEE FOUNDATIONCHAPTER - ALGEBRAEXERCISE - NCERT SECTION (EXERCISE - 11.3)
24 Videos
- BASIC GEOMETRICAL IDEASBOOK - MTG IIT JEE FOUNDATIONCHAPTER - BASIC GEOMETRICAL IDEASEXERCISE - OLYMPIAD/HOTS CORNER
10 Videos
Similar Questions
(a) Given Munnu’s age to be x years, can you guess what (x+2) may show? (Hint : Think of Munnu’s younger brother.) Can you guess what (x+4) may show? What (3x+7) may show? (b) Given Sara’s age today to be y years. Think of her age in the future or in the past. What will the following expression indicate? y+7,y−3,y+(4)12,(2)12. (c) Given n students in the class like football, what may 2 n show ? What may n2 show ? (Hint : Think of games others than football )Type here in ASCII with maths in back tick :
View SolutionIn a class of 35 students, 24 like to play cricket and 16 like to play football. Also, each student likes to play at least one of the two games. How many students like to play both cricket and football?
View Solution
Knowledge Check
In a group of 50 students ,30 like Basketball ,20 like football and 10 like neither of the games .How many like both the game ?
The following steps are involved in solving the above problem .Arrange them in sequential order.
(A) n(B∩F)=50−40=10
⇒40=50−n(B∩F)
( C ) Let n(B) = 30 ,n(F)=20 and n(B∪F)=50−10=40
We know that n(B∪F)=n(B)+n(F)−n(B∩F)ACDBABCBDACADBCDBCDAIn a group of 50 students ,30 like Basketball ,20 like football and 10 like neither of the games .How many like both the game ?
The following steps are involved in solving the above problem .Arrange them in sequential order.
(A) n(B∩F)=50−40=10
⇒40=50−n(B∩F)
( C ) Let n(B) = 30 ,n(F)=20 and n(B∪F)=50−10=40
We know that n(B∪F)=n(B)+n(F)−n(B∩F)ACDBABCBDACADBCDBCDAA class has 50 student ,each student likes either cricket or football or both .Sixteen students like both the games .Find the number of students who like exactly one game .
A34B32C38D36
In a class of 35 students, 24 like to play cricket and 16 like to play football. Also, each student likes to play at least one of the two games. How many students like to play both cricket and football?
View SolutionIn a class of 35 students, 24 students like cricket and 16 like football. If each student plays atleast one game, find how many students like both games ?
View SolutionA survey of students was made to know which game they like. The data obtained in the survey is presented in the following pie diagram. If the total number of students are 1000,
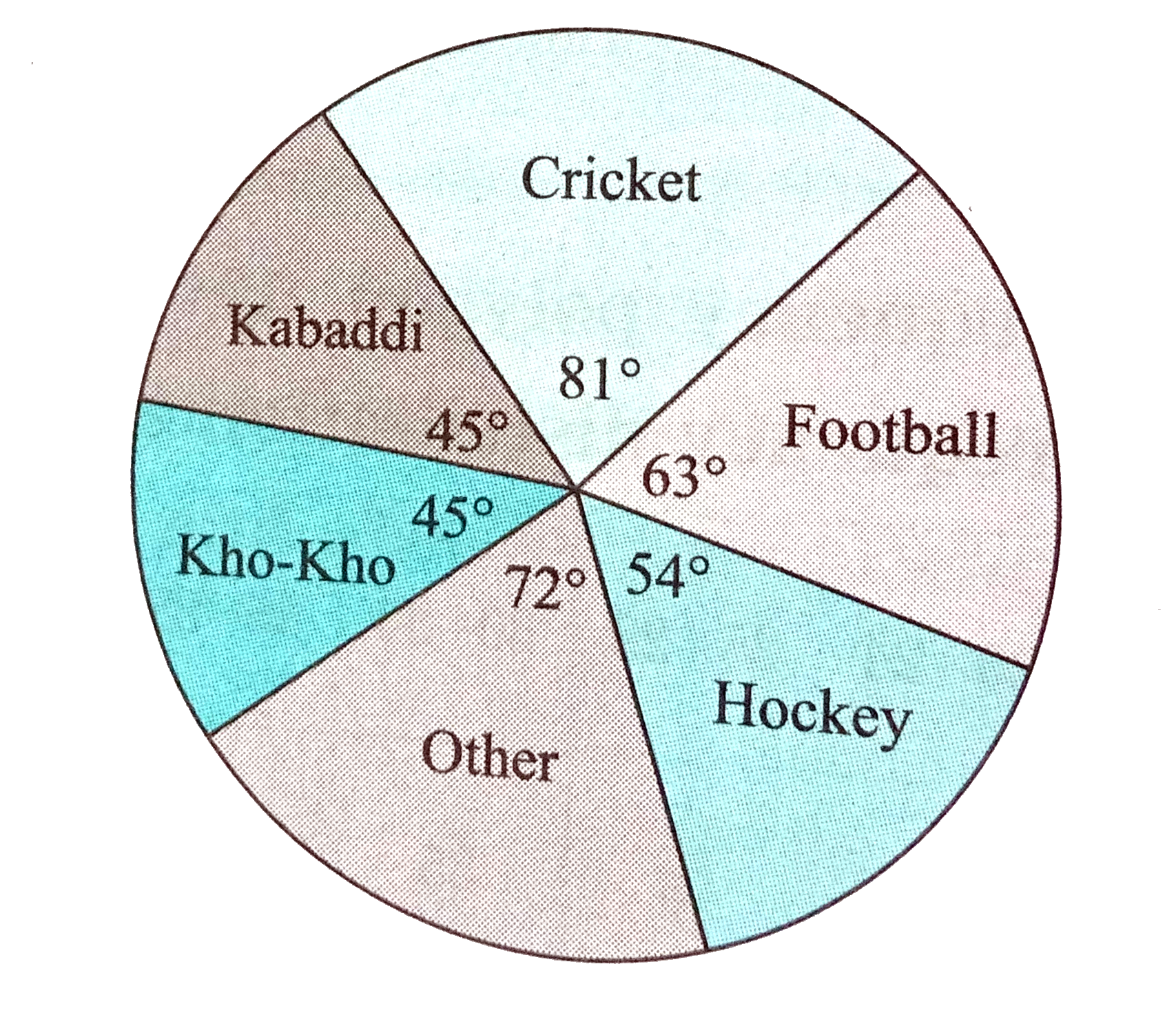
(1) how many students like cricket ?
(2) how many studetns like football ?
(3) how many students prefer other games ?
View SolutionIf 60% people in a city like cricket, 30% like football and remaining like other games. What percent like the other games? If the total number of people is 56 lakhs, find the exact number who like each type of game.
View SolutionThere are 70 students in a class. Of them, 50 students like cricket. 35 like both cricket and football and some like only football. Select the Venn diagram that correctly represents the given information.
View Solution
