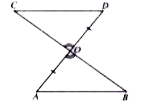
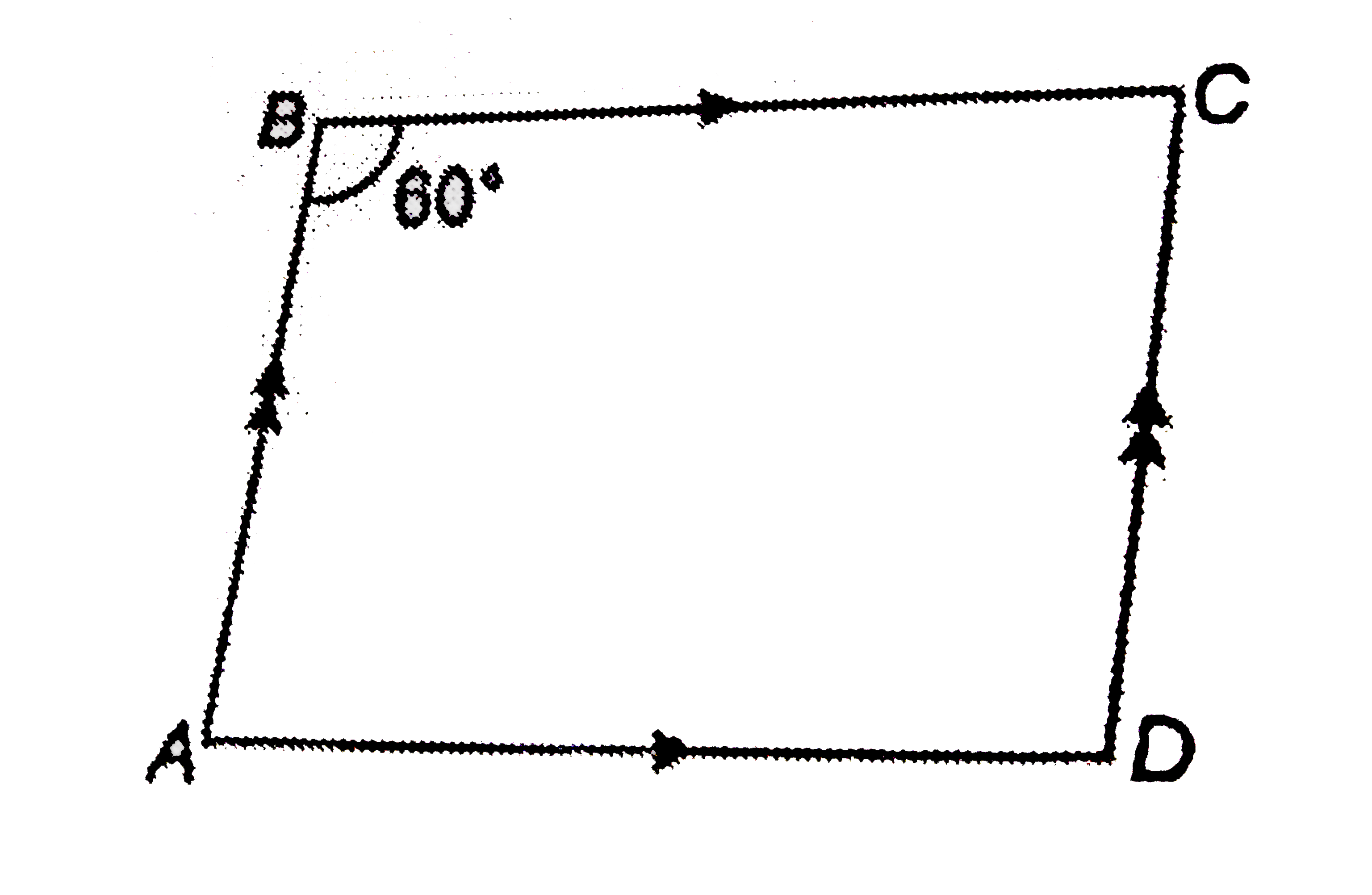Given that in the figure, AB||CD and AB=CD where AD and BC intersect at point O. What is the congruence condition that proves △OAB≅△ODC?
Text Solution
The correct Answer is:AB=CD
|
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLESBOOK - ICSECHAPTER - CONGRUENCE OF TRIANGLESEXERCISE - EXERCISE 13.1
7 Videos
- CONGRUENCE OF TRIANGLESBOOK - ICSECHAPTER - CONGRUENCE OF TRIANGLESEXERCISE - EXERCISE 13.2
11 Videos
- CONGRUENCEBOOK - ICSECHAPTER - CONGRUENCEEXERCISE - EXERCISE 21
23 Videos
- CONSTRUCTION BOOK - ICSECHAPTER - CONSTRUCTION EXERCISE - EXERCISE
18 Videos
Similar Questions
Knowledge Check

If, in the figure above, CD=1, AB=-2, and AD=6, then BC=A5B9C2+√5D3√5
In the given figure, AB∣∣CD and AB=CD, prove that: ΔAOB≅ΔDOC

View SolutionIn Figure, if AB=AC and BE=CD, prove that AD=AE.
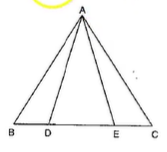
View SolutionIn the given figure. AB∣CDandO is the midpoint of AD.
View SolutionIn the following figure, OA=OC and AB=BC.
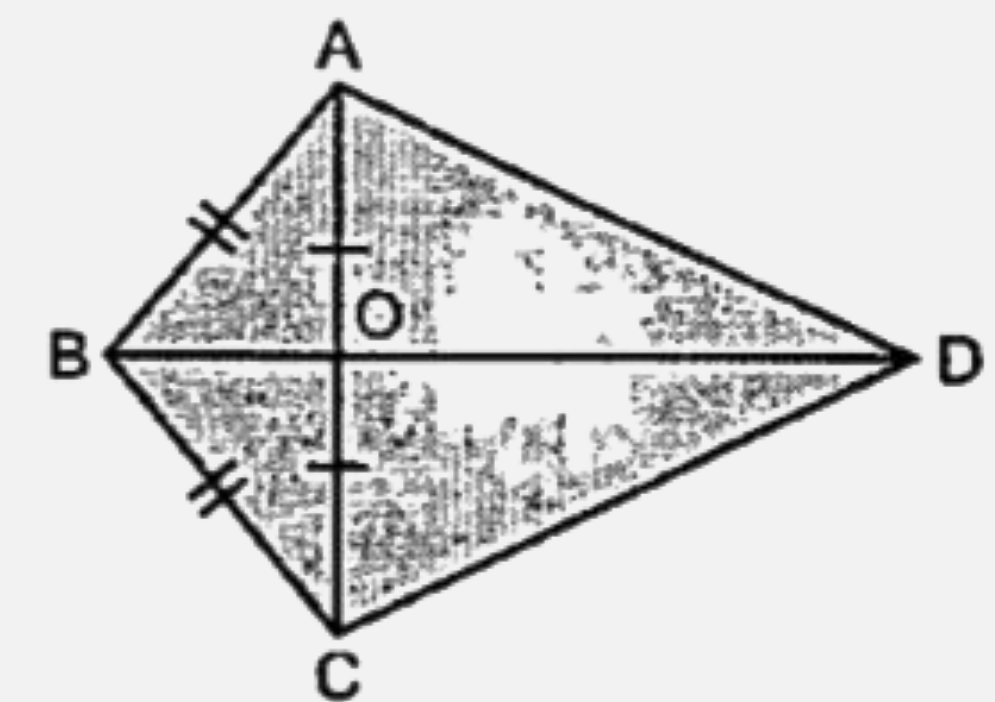
Prove that :
AD=CD
View SolutionIn the figure AB || CD, AD and BC intersect at o and O is mid-point of AD. Show that
(i) ΔAOB≅ΔDOCand(ii)OB=OC.
View Solution
In the above figure, AB=BC=8 cm and AD=CD=10 cm, which axiom best proves the congruence of ΔABDandΔCBD?
View SolutionIn figure, AB || DC and AB = CD.
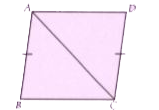
Is ΔABC≅ΔCDA by SAS congruence condition?
View Solution