Given the equatins above, what is the value of x+y ?
The correct Answer is:12
To solve the given equations and find the value of x+y, we will follow these steps:
Step 1: Write down the equations
The given equations are:
1. 3x=4y−13 (Equation 1)
2. 3y=31−2x (Equation 2)
Step 2: Rearrange the equations
We can rearrange both equations to express them in a standard form.
From Equation 1:
3x−4y=−13(Rearranged Equation 1)
From Equation 2:
2x+3y=31(Rearranged Equation 2)
Step 3: Eliminate one variable
To eliminate x, we can multiply the first equation by 2 and the second equation by 3 to make the coefficients of x the same.
Multiplying the rearranged Equation 1 by 2:
2(3x−4y)=2(−13)⟹6x−8y=−26(Equation 3)
Multiplying the rearranged Equation 2 by 3:
3(2x+3y)=3(31)⟹6x+9y=93(Equation 4)
Step 4: Add the equations
Now we can add Equation 3 and Equation 4:
(6x−8y)+(6x+9y)=−26+93
This simplifies to:
12x+y=67
Step 5: Solve for y
From the equation 12x+y=67, we can express y in terms of x:
y=67−12x(Equation 5)
Step 6: Substitute back to find x
Now we can substitute y back into one of the original equations to find x. Let's use Equation 1:
3x=4(67−12x)−13
Expanding this gives:
3x=268−48x−13
Combining like terms:
3x+48x=255⟹51x=255⟹x=5
Step 7: Find y
Now substitute x=5 back into Equation 5 to find y:
y=67−12(5)=67−60=7
Step 8: Calculate x+y
Finally, we can find x+y:
x+y=5+7=12
Final Answer
The value of x+y is 12.
---
The given equations are:
1. 3x=4y−13 (Equation 1)
2. 3y=31−2x (Equation 2)
We can rearrange both equations to express them in a standard form.
3x−4y=−13(Rearranged Equation 1)
2x+3y=31(Rearranged Equation 2)
To eliminate x, we can multiply the first equation by 2 and the second equation by 3 to make the coefficients of x the same.
2(3x−4y)=2(−13)⟹6x−8y=−26(Equation 3)
3(2x+3y)=3(31)⟹6x+9y=93(Equation 4)
Now we can add Equation 3 and Equation 4:
(6x−8y)+(6x+9y)=−26+93
This simplifies to:
12x+y=67
From the equation 12x+y=67, we can express y in terms of x:
y=67−12x(Equation 5)
Now we can substitute y back into one of the original equations to find x. Let's use Equation 1:
3x=4(67−12x)−13
Expanding this gives:
3x=268−48x−13
Combining like terms:
3x+48x=255⟹51x=255⟹x=5
Now substitute x=5 back into Equation 5 to find y:
y=67−12(5)=67−60=7
Finally, we can find x+y:
x+y=5+7=12
The value of x+y is 12.
Topper's Solved these Questions
Similar Questions
Knowledge Check
2x − y = 8
x + 2y = 4
For the system of equations above, what is the value of x + y ?A–1B4C5D202x-3y=-14
3x-2y=-6
If (x ,y) is a solution to the system of equations above, what is the value of x − y ?A−20B−8C−4D87x+3y=8
6 −3 =5
For the solution (x, y) to the system of equations above, what is the value of x − y ?A−43B23C43D223
−x+y=−3.5
x+3y=9.5
If (x, y) satisfies the system of equations above, what is the value of y ?
View Solution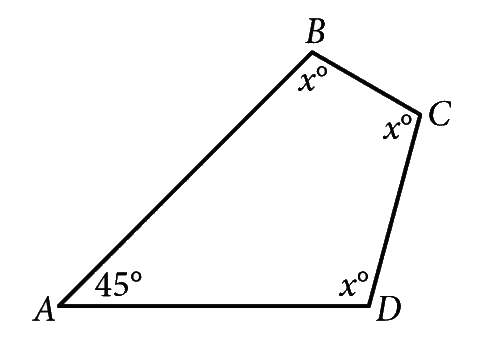
In the figure above, what is the value of x ?
View Solution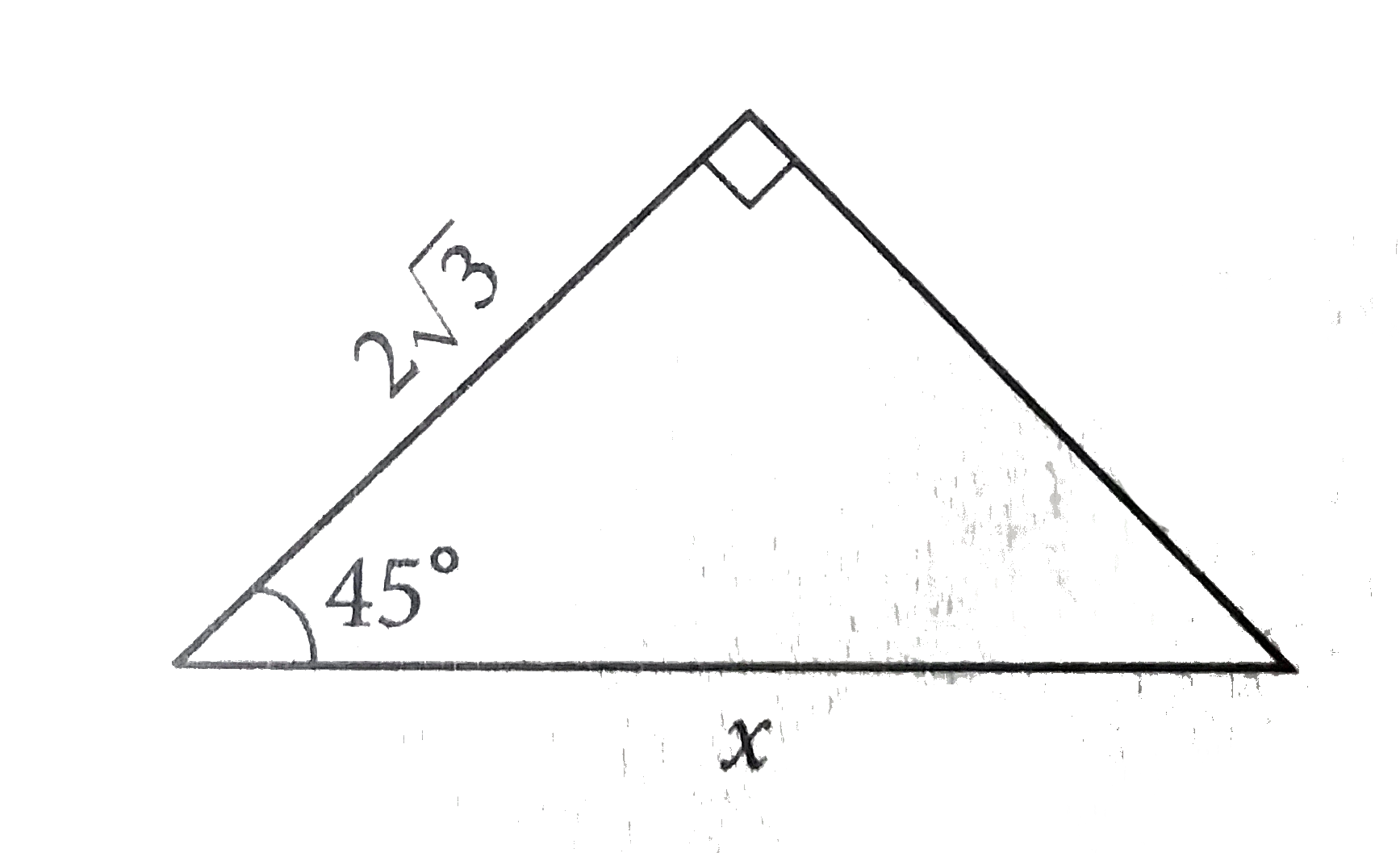
In the figure above, what is the value of x?
View Solutionxy=6
If (x,y) is the solution to the system of equations above, what is the value of y ?
View Solution
In the figure above, what is the value of y?
View Solution
