Given the straight line x+51=y+34=z−6−9. What are its direction rations?Solution in Malayalam
Step by step video & image solution for Given the straight line (x+5)/1=(y+3)/4=(z-6)/-9. What are its direction rations? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THREE DIMENSIONAL GEOMETRYBOOK - BODY BOOKS PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - EXERCISE
5 Videos
- RELATIONS AND FUNCTIONSBOOK - BODY BOOKS PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE
10 Videos
- VECTOR ALGEBRABOOK - BODY BOOKS PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - EXERCISE
1 Videos
Similar Questions
Find the shortest distance between the lines l1 and l2 ¯r=ˆi+ˆj+λ(2ˆi−ˆj+k) and
¯r=2ˆi+ˆj−ˆk+μ⋅(3ˆi−5ˆj+2ˆk)
View SolutionIf the mapping of f and g are given by F={(1,2),(3,5),(4,1) ang g={(2,3),(5,1),(1,3)} then write fog.
View SolutionIf →a and →b are unit vectors inclined at an angle θ,then prove that sin(θ2)=12∣∣→a−→b∣∣
View SolutionFind the distance of a point (2,4,−1) from the line
x+51=y+34=z−6−9.
View Solutionएक सरल रेखा के कार्तीय समीकरण x−53=y−47=z−62 है| रेखा के दिक् अनुपात है
View Solutionएक सरल रेखा का कार्तिए समीकरण x+33=y−59=z+42 है! एक सरल रेखा का सदिश समीकरण ज्ञात कीजिए
View SolutionIn the adjoining figure, x:y:z=5:4:6. If XOY is a straight line, find the values of x, y and z.
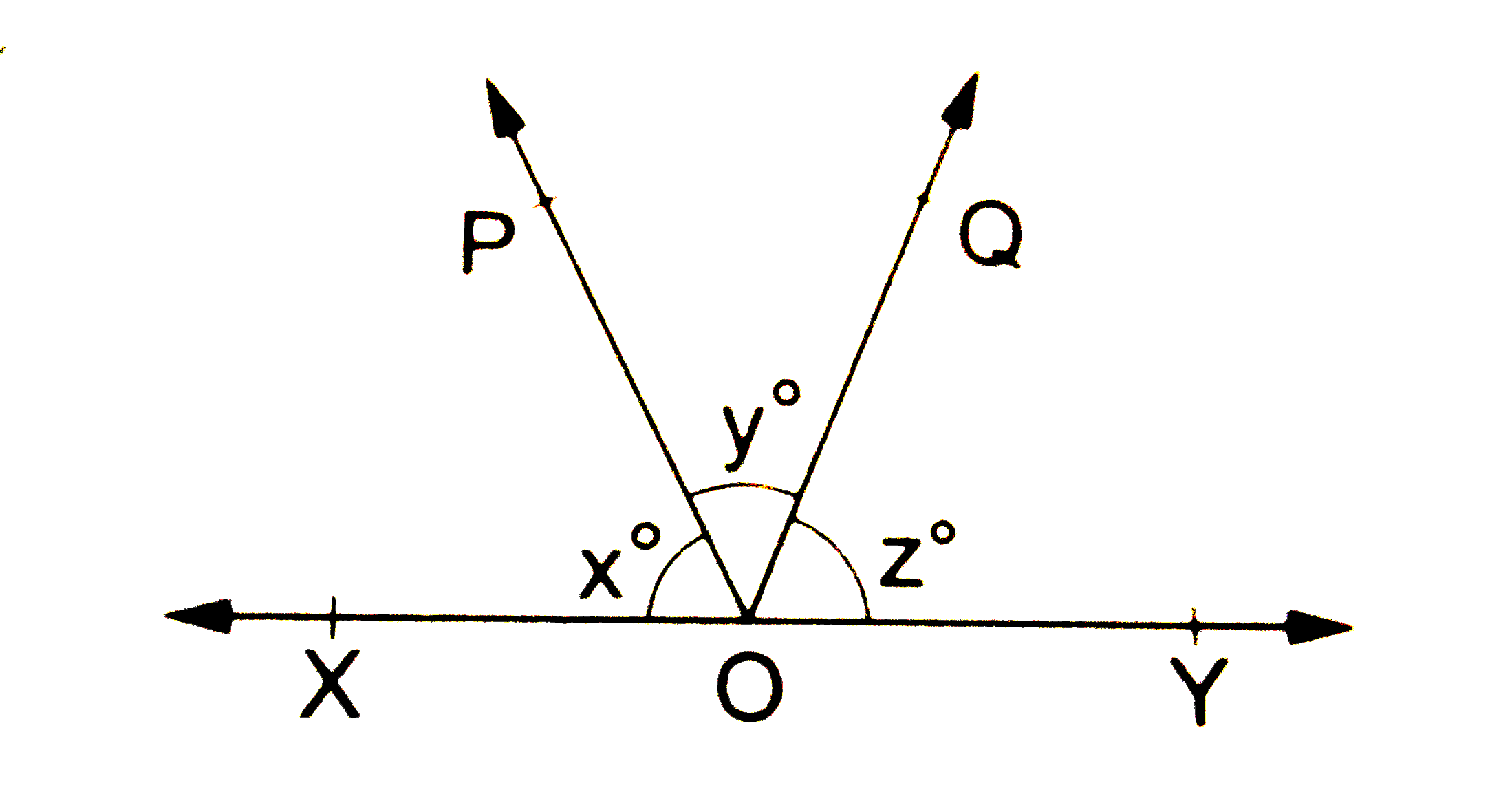
View SolutionThe foot of the perpendicular form (2,4,−1) to the line x+5=14(y+3)=−19(z−6) is
View SolutionThe foot of the perpendicular from (2,4,-1) to the line x+51=y+34=z−6−9 is
View SolutionThe cartesian equation of a straight line is x−34=y+25=z−43, its vector form will be -
View SolutionThe straight lines x−32=y+54=z−1−13andx+13=y−45=z+22 are
View Solutionबिन्दु (2, 4, -1) से सरल रेखा x+51=y+34=z−6−9 की लम्बवत दूरी है
View Solutionx−72=y+63=z+2−4 ও 2−x−1=y−95=z−124 সরলরেখা দুটির অন্তর্ভুক্ত কোণ নির্ণয় করো।
View Solutionx+51=y+34=z−6−9 সরলরেখার ওপর A(2,4,−1) বিন্দু থেকে অঙ্কিত লম্বের পাদবিন্দুর স্থানাঙ্ক হয়—
View Solutionএকটি সরলরেখার সমীকরণ হয় 4−x2=y+32=z+21। সরলরেখাটির সমান্তরাল একটি সরলরেখার direction cosines নির্ণয় করো।
View Solution
