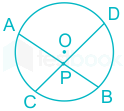
Given two concetric circles with centre O. A line cut the circle at A,B,C and D respectively. If AB=10cm, then find the length of CD.
The correct Answer is:10cm
To solve the problem of finding the length of CD given that AB = 10 cm in two concentric circles with center O, we can follow these steps:
1. Understand the Configuration: We have two concentric circles with the same center O. A line intersects these circles at points A, B, C, and D.
2. Identify the Segments: The line segment AB is the chord of the outer circle, and the line segment CD is the chord of the inner circle.
3. Use the Property of Chords in Concentric Circles: In concentric circles, if a line intersects both circles, the lengths of the chords created by that line will be equal. This is because the distance from the center to the line is the same for both circles.
4. Given Information: We know that the length of the chord AB in the outer circle is 10 cm.
5. Conclusion: Since the lengths of the chords AB and CD are equal in concentric circles, we can conclude that the length of chord CD is also 10 cm.
Final Answer:
The length of CD is 10 cm.
---
The length of CD is 10 cm.
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PART-B2videos
CIRCLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PART-C4videos
CIRCLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PART-A (Fill in the Blanks)3videos
CIRCLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - PRACTICE TEST2videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - PRACTICE TEST9videos
CO-ORDINATE GEOMETRY
Similar Questions
Two same circles of radius 5 cm has a direct tangent AB and a transversal CD which touch circle at A, B and C, D respectively. If CD = 24 cm then find the length of AB (in cm)?
View SolutionIn the adjoining figure,O is the centre of two concentric circles. The chord AB of larger circle intersects the smaller circle at C and D.
(i) Find AC:BD.
(ii) If AC=2cm, then find the length of BD.
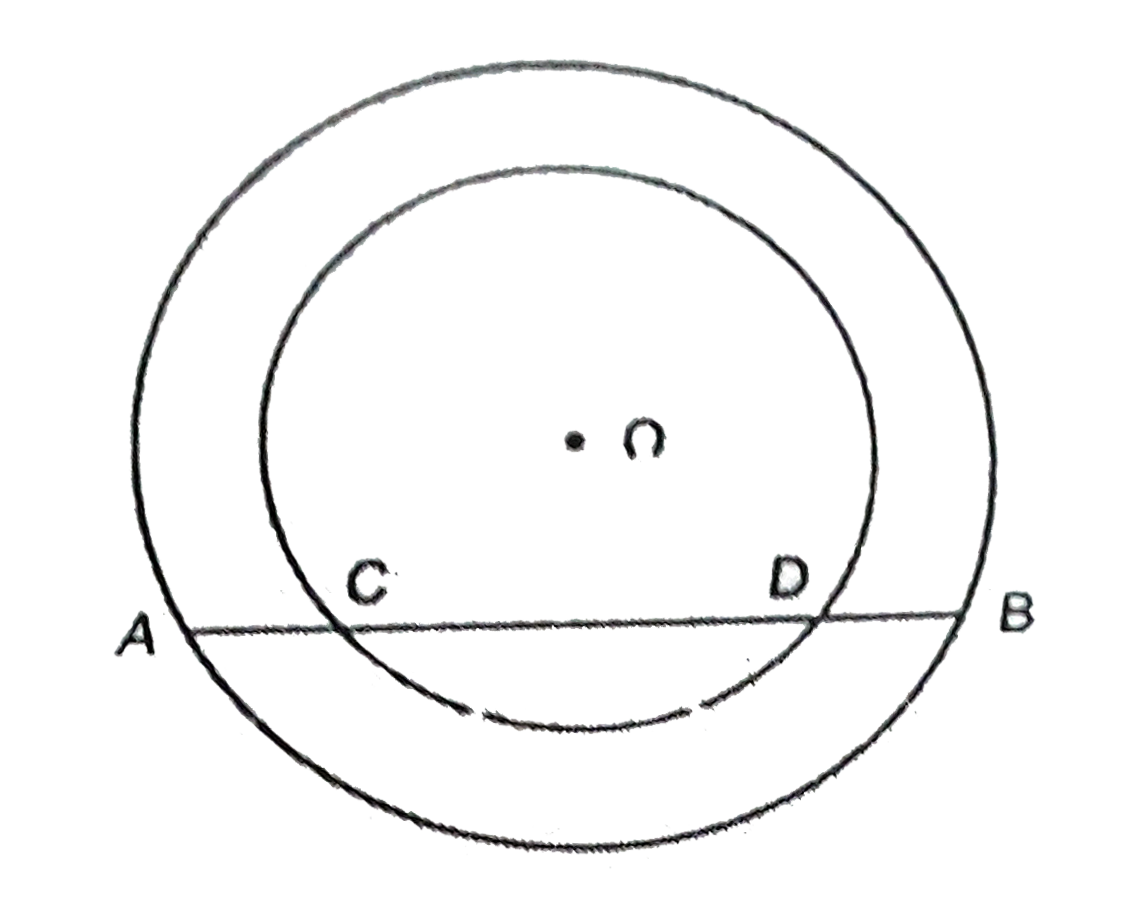 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
AC is transverse common tangent to two circles with centres P and Q and radii 6 cm and 3 cm at the point A and C respectively. If AC cuts PQ at the point B and AB= 8cm then the length of PQ is:
A13 cmB12 cmC10 cmD15 cm - Question 2 - Select One
The radius of two concentric circles are 17cm and 10cm. A straight line ABCD intersects the larger circle at the point A and D and intersects the smaller circle at the points B and C. If BC = 12 cm, then the length of AD (in cm) is :
A20B24C30D34
There are two concentric circles with centre O and a chord AB of outer circle cut the inner circle at C and D. If distance of chord to centre is 3 cm, outer radius is 13 cm and inner radius is 7 cm, then length of AC is-
View SolutionIn the figure, the circles with centeres A and B touch each other at E. Line l is a common tangent which touches the circles at C and D respectively. Find the length of seg CD, if the radii of the circle are 4 cm, 6 cm.
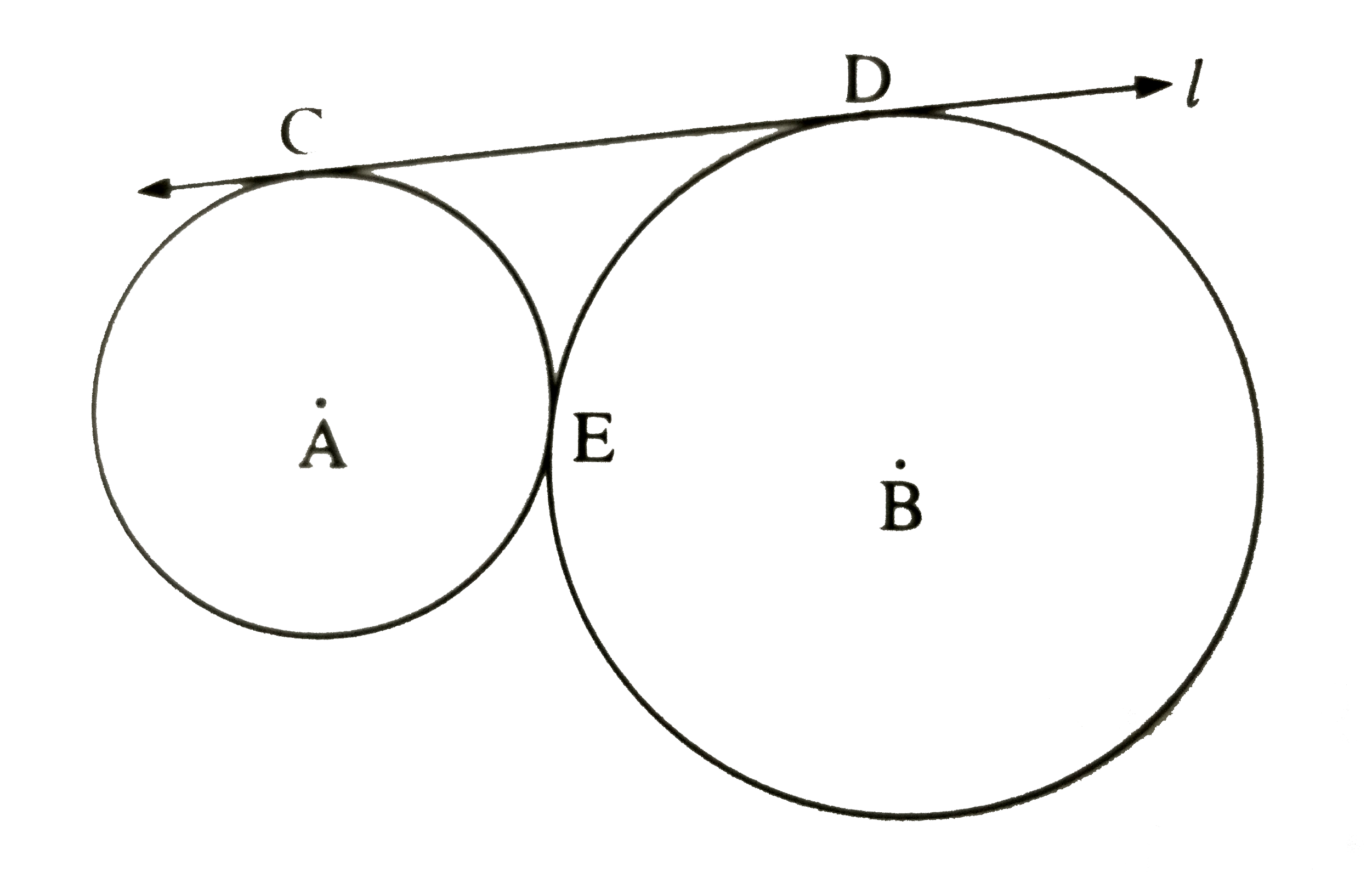 View Solution
View SolutionIn the adjoining figure, O is the centre of the centre of the circle. If diameter AC=26cm and chord AB=10cm, then find the distances of the chord AB from the centre of the circle.
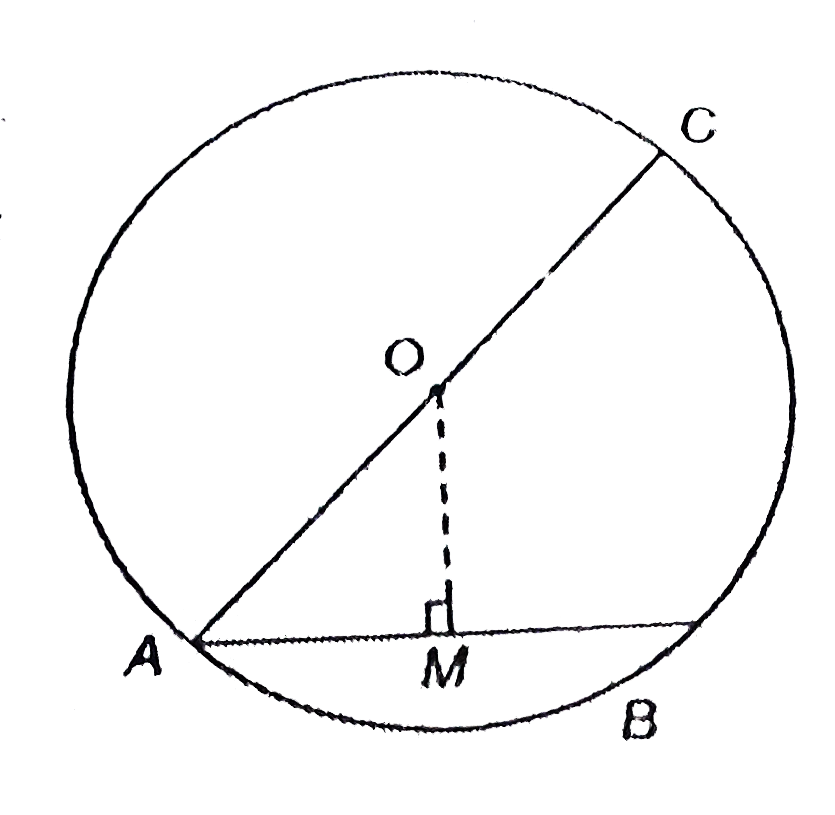 View Solution
View SolutionIn the given figure, O is the centre of a circle such that OA = 5 cm, AB = 8 cm and OD⊥AB meeting AB at C. Find the length of CD.
View SolutionIf a line intersects two concenteric circles (circles with the same centre) with center O at A,B,C and D, prove that AB=CD (see figure).
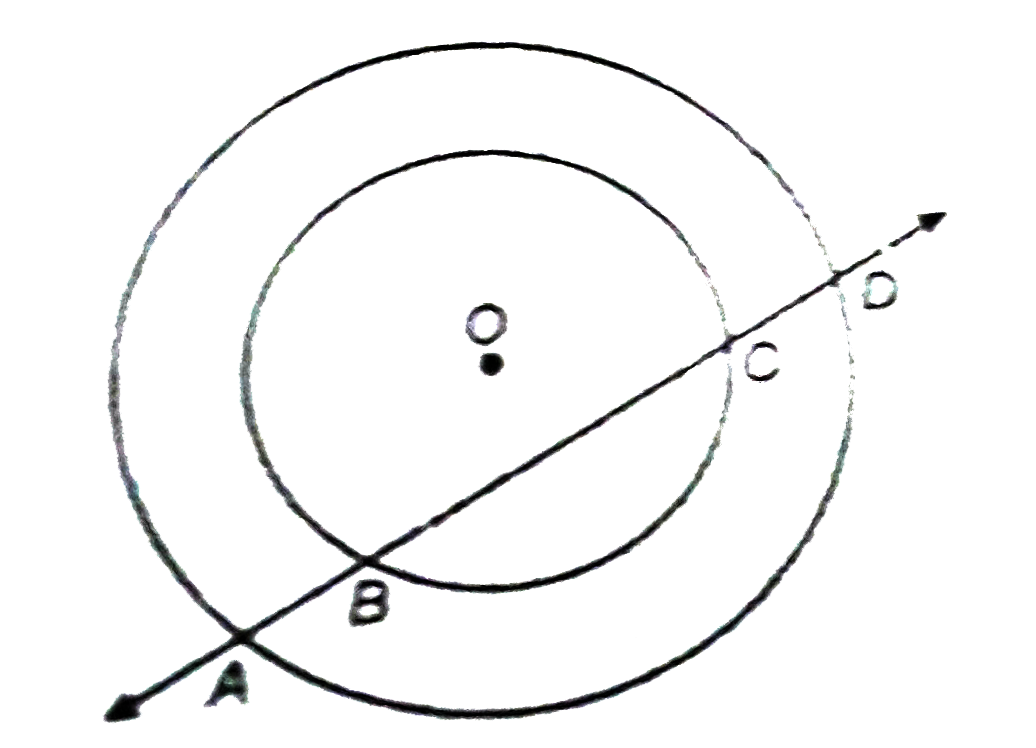 View Solution
View SolutionIn the given figure, O is the centre of the circle. Its two chords AB and CD intersect each other at the point p within the circle. If AB=15cm,PB=9cm, then find the length of PD.
 View Solution
View Solution

