Given z is a complex number with modulus 1. Then the equation (1+ia1−ia)4=z has
all roots real and distinct
two roots real and two imaginary
three roots real and one imaginary
one root real and three imaginary
The correct Answer is:A
To solve the equation (1+ia1−ia)4=z given that z is a complex number with modulus 1, we will follow these steps:
Step 1: Analyze the given equation
We start with the equation:
(1+ia1−ia)4=z
Since z has a modulus of 1, we can deduce that the modulus of the left-hand side must also be 1.
Step 2: Calculate the modulus of the left-hand side
We need to find the modulus of 1+ia1−ia:
Modulus=|1+ia||1−ia|
Calculating the modulus of the numerator and denominator:
- For 1+ia:
|1+ia|=√12+a2=√1+a2
- For 1−ia:
|1−ia|=√12+a2=√1+a2
Thus, we have:
|1+ia||1−ia|=√1+a2√1+a2=1
Step 3: Raise the modulus to the power of 4
Now, raising the modulus to the power of 4:
(|1+ia||1−ia|)4=14=1
This confirms that the left-hand side has a modulus of 1.
Step 4: Set the modulus equal to the modulus of z
Since we know that the modulus of z is also 1, we have:
1=|z|=1
This condition is satisfied.
Step 5: Analyze the argument of the complex number
Next, we need to consider the argument of the complex number:
1+ia1−ia
Using the property of arguments:
arg(1+ia1−ia)=arg(1+ia)−arg(1−ia)
Calculating the arguments:
- For 1+ia:
arg(1+ia)=tan−1(a1)=tan−1(a)
- For 1−ia:
arg(1−ia)=tan−1(−a1)=−tan−1(a)
Thus:
arg(1+ia1−ia)=tan−1(a)−(−tan−1(a))=2tan−1(a)
Step 6: Set the argument equal to z
Now, we have:
arg((1+ia1−ia)4)=4⋅arg(1+ia1−ia)=8tan−1(a)
This means:
8tan−1(a)=arg(z)
Since z has modulus 1, its argument can take any value.
Conclusion
The equation (1+ia1−ia)4=z has solutions for all real values of a. Therefore, the solutions are real and distinct.
We start with the equation:
(1+ia1−ia)4=z
Since z has a modulus of 1, we can deduce that the modulus of the left-hand side must also be 1.
We need to find the modulus of 1+ia1−ia:
Modulus=|1+ia||1−ia|
Calculating the modulus of the numerator and denominator:
- For 1+ia:
|1+ia|=√12+a2=√1+a2
- For 1−ia:
|1−ia|=√12+a2=√1+a2
Thus, we have:
|1+ia||1−ia|=√1+a2√1+a2=1
Now, raising the modulus to the power of 4:
(|1+ia||1−ia|)4=14=1
This confirms that the left-hand side has a modulus of 1.
Since we know that the modulus of z is also 1, we have:
1=|z|=1
This condition is satisfied.
Next, we need to consider the argument of the complex number:
1+ia1−ia
Using the property of arguments:
arg(1+ia1−ia)=arg(1+ia)−arg(1−ia)
Calculating the arguments:
- For 1+ia:
arg(1+ia)=tan−1(a1)=tan−1(a)
- For 1−ia:
arg(1−ia)=tan−1(−a1)=−tan−1(a)
Thus:
arg(1+ia1−ia)=tan−1(a)−(−tan−1(a))=2tan−1(a)
Now, we have:
arg((1+ia1−ia)4)=4⋅arg(1+ia1−ia)=8tan−1(a)
This means:
8tan−1(a)=arg(z)
Since z has modulus 1, its argument can take any value.
The equation (1+ia1−ia)4=z has solutions for all real values of a. Therefore, the solutions are real and distinct.
Topper's Solved these Questions
- COMPLEX NUMBERS BOOK - ML KHANNACHAPTER - COMPLEX NUMBERS EXERCISE - Problem Set (2) (True and False )
4 Videos
- COMPLEX NUMBERS BOOK - ML KHANNACHAPTER - COMPLEX NUMBERS EXERCISE - Problem Set (2) (Fill in the blanks)
2 Videos
- COMPLEX NUMBERS BOOK - ML KHANNACHAPTER - COMPLEX NUMBERS EXERCISE - Problem Set (1) (True and False)
5 Videos
- CO-ORDINATE GEOMETRY OF THREE DIMENSIONBOOK - ML KHANNACHAPTER - CO-ORDINATE GEOMETRY OF THREE DIMENSIONEXERCISE - SELF ASSIGNMENT TEST
11 Videos
- CONCEPTS OF SET THEORY BOOK - ML KHANNACHAPTER - CONCEPTS OF SET THEORY EXERCISE - Self Assessment Test
13 Videos
Similar Questions
Knowledge Check
The complex number z =x+iy which satisfies the equation ∣∣∣z−3iz+3i∣∣∣=1, then on
Athe X-axisBthe straight line y = 3Ca circle passing through originDNone of the aboveThe complex number z =x+iy which satisfies the equation ∣∣∣z−3iz+3i∣∣∣=1, then on
Athe X-axisBthe straight line y = 3Ca circle passing through originDNone of the aboveThe complex numbers z = x + iy which satisfy the equation ∣∣∣z−5iz+5i∣∣∣=1, lie on
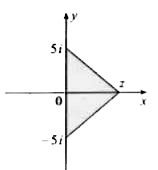 Athe x-axisBthe straight line y = 5Ca circle passing through the originDnone of these
Athe x-axisBthe straight line y = 5Ca circle passing through the originDnone of these
Find a complex number z satisfying the equation z+√2|z+1|+i=0.
View SolutionIf z is a complex number satisfying the relation |z+1|=z+2(1+i), then z is
View SolutionIf z is a complex number which simultaneously satisfies the equations
3|z−12|=5|z−8i| and |z−4|=|z−8|, where i=√−1, then Im(z) can be
View SolutionThe complex number z satisfying the equation |z−i|=|z+1|=1
View SolutionIfa complex number z has modulus 1 and argument π3, then z2+z
View Solution
