Go back to Pascal's triangle.
Line 1:1=11∘
Line 2:1,1=111
Line 3:1,2,1=112
Make a conjecture about Line 4 and Line 5. Does your conjecture hold ? Does your conjecture hold for Line 6 too ? Solution in Kannada
Step by step video & image solution for Go back to Pascal's triangle. Line 1 : 1 = 11^(@) Line 2 : 1, 1 = 11^(1) Line 3 : 1, 2, 1 = 11^(2) Make a conjecture about Line 4 and Line 5. Does your conjecture hold ? Does your conjecture hold for Line 6 too ? by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPENDIX ABOOK - SUBHASH PUBLICATIONCHAPTER - APPENDIX AEXERCISE - EXERCISE A 1.4
10 Videos
- APPENDIX ABOOK - SUBHASH PUBLICATIONCHAPTER - APPENDIX AEXERCISE - EXERCISE A 1.4
10 Videos
- APPENDIX 2 INTRODUCTION TO MATHEMATICAL MODELLING BOOK - SUBHASH PUBLICATIONCHAPTER - APPENDIX 2 INTRODUCTION TO MATHEMATICAL MODELLING EXERCISE - EXERCISE A2.1
4 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - SUBHASH PUBLICATIONCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE 11.4
3 Videos
Similar Questions
Find counter - examples to disprove the following statements :
If the corresponding angles in two triangles are equal, then the triangles are congruent.
View SolutionFind counter - examples to disprove the following statements :
If the corresponding angles in two triangles are equal, then the triangles are congruent.
View SolutionSuppose a company needs a computer for some period of time. The company can either hire a computer for Rs. 2,000 per month or buy one for Rs 25,000. If the company has to use the computer for a long period, the company will pay such a high rent, that buying a computer has to use the computer will be cheaper. Find the number of months beyond which it will be cheaper to buy a computer.
View SolutionParallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View SolutionThe prejection of the line segment joining the poing (1,−1,3) and (2,−4,11) on the line joining the points (−1,2,3) and (3,−2,10), is ……
View SolutionEquations of the line through (4,−5,6) and perpendicular to the lines x−111=y+6−3=z−50and x−15=y−22=z−811 are
View SolutionLook at the following pattern :
12=1
112=121
1112=12321
11112=1234321
111112=123454321
Make a conjecture about each of the following :
1111112=
11111112=
Check if your conjecture is true.
View SolutionNote the Pascal triangle: line 1: 1 = 11^@ Row 2: 11 = 11^1 Row 3: 121 = 11^2 Create hypotheses for line 4 and base line 5. Check whether these hypotheses are sustainable. Similarly to line 6, test your hypothesis.
View SolutionGo back to Pascal's triangle . Line -1 : 1=11^(0) Line -2 : 11 = 11^(1) Line-3 : 121 = 11^(2) Make a conjecture about Line-4 and Line-5 . Does your conjecture hold ? Does your conjecture hold for Line -6 too ?
View SolutionLook at the following pattern: 1^(2) = 1 11^(2) =121 111^2 = 12321 1111^(2)=1234321 11111^2 = 123454321 Make a conjecture about about each of the following : 111111^2=.............. 1111111^2=........... Check if your conjecture is true .
View SolutionGo back to Pascal's triangle . Line -1 : 1=11^(0) Line -2 : 11 = 11^(1) Line-3 : 121 = 11^(2) Make a conjecture about Line-4 and Line-5 . Does your conjecture hold ? Does your conjecture hold for Line -6 too ?
View SolutionLook at the following pattern: 1^(2) = 1 11^(2) =121 111^2 = 12321 1111^(2)=1234321 11111^2 = 123454321 Make a conjecture about about each of the following : 111111^2=.............. 1111111^2=........... Check if your conjecture is true .
View SolutionLook at the following pattern:
12=1
112=121
1112=12321
11112=1234321
111112=123454321
Make a conjecture about about each of the following :
1111112=..............
11111112=...........
Check if your conjecture is true .
View SolutionGo back to Pascal's triangle .
Line -1 : 1=110
Line -2 : 11=111
Line-3 : 121=112
Make a conjecture about Line-4 and Line-5 .
Does your conjecture hold ? Does your conjecture hold for Line -6 too ?
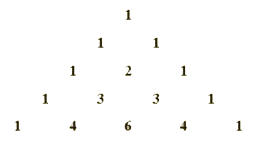
View SolutionLook at the following pattern:
12=1
112=121
1112=12321
11112=1234321
111112=123454321
Make a conjecture about about each of the following :
1111112=..............
11111112=...........
Check if your conjecture is true .
View Solution
