How many diagonals are there in a polygon of n sides?
A
n(n−1)2
B
n(n−3)2
C
n(n+1)2
D
none of these
Video Solution
Text Solution
The correct Answer is:B
A polygon of n sides has n vertices. By joining any two vertices of a polygon, we obtain either a side or a diagonal of the polygon. Number of line segments obtained by joining the vertices of a n sided polygon taken two at a time
= Number of ways of selecting 2 out of n=nC2=n(n−1)2
Out of these lines, n lines are the sides of the polygon.
∴ Number of diagonals of the polygon =n(n−1)2−n.
=n(n−3)2
|
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Section I - Solved Mcqs
111 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Section II - Assertion Reason Type
9 Videos
- PARABOLABOOK - OBJECTIVE RD SHARMACHAPTER - PARABOLAEXERCISE - Chapter Test
30 Videos
- PROBABILITY BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Chapter Test
45 Videos
Similar Questions
Knowledge Check
How many diagonals are there in a polygon having 12 sides ?
A12B24C36D54The number of diagonals in a polygon of m sides is
A12!m(m−5)B12!m(m−1)C12!m(m−3)D12!m(m−2)The number of diagonals of a polygon of n sides is
An(n−1)2Bn(n−3)2C(n−1)(n−2)2Dnone of these
Find the numbers of diagonals in the polygon of n sides.
View SolutionFind the number of diagonals in the convex polygon of n sides .
View SolutionA polygon is entirely made up of straight lines only. A hexagon ABCDEF is a six sided polygon.
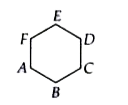
How many diagonals are there in the hexagon?
View SolutionThe number of pairs of diagonals of a regular polygon of 10 sides that are parallel are
View SolutionThe number of diagonals of a polygon of 15 sides is
View Solution