How many different words can be formed by using all the letters of the word ALLAHABAD?
30
(9!)
(9!)/(2!)
(9!)/(2! 4!)
The correct Answer is:D
To find the number of different words that can be formed using all the letters of the word "ALLAHABAD", we can follow these steps:
Step 1: Count the total number of letters
The word "ALLAHABAD" consists of 9 letters.
Step 2: Identify the frequency of each letter
In the word "ALLAHABAD":
- A appears 4 times
- L appears 2 times
- H appears 1 time
- B appears 1 time
- D appears 1 time
Step 3: Use the formula for permutations of multiset
The formula to find the number of distinct permutations of a set of items where there are repetitions is given by:
Number of arrangements=n!p1!×p2!×…×pk!
Where:
- n is the total number of items,
- p1,p2,…,pk are the frequencies of the repeated items.
Step 4: Apply the formula
In our case:
- n=9 (total letters)
- p1=4 (for A)
- p2=2 (for L)
- p3=1 (for H)
- p4=1 (for B)
- p5=1 (for D)
Thus, the number of different arrangements is:
Number of arrangements=9!4!×2!×1!×1!×1!
Step 5: Calculate the factorials
Now we calculate the factorials:
- 9!=362880
- 4!=24
- 2!=2
- 1!=1 (for H, B, and D)
Step 6: Substitute the values into the formula
Now substituting the values into the formula:
Number of arrangements=36288024×2×1×1×1=36288048=7560
Final Answer
Therefore, the total number of different words that can be formed using all the letters of the word "ALLAHABAD" is 7560.
---
The word "ALLAHABAD" consists of 9 letters.
In the word "ALLAHABAD":
- A appears 4 times
- L appears 2 times
- H appears 1 time
- B appears 1 time
- D appears 1 time
The formula to find the number of distinct permutations of a set of items where there are repetitions is given by:
- n is the total number of items,
- p1,p2,…,pk are the frequencies of the repeated items.
In our case:
- n=9 (total letters)
- p1=4 (for A)
- p2=2 (for L)
- p3=1 (for H)
- p4=1 (for B)
- p5=1 (for D)
Now we calculate the factorials:
- 9!=362880
- 4!=24
- 2!=2
- 1!=1 (for H, B, and D)
Now substituting the values into the formula:
Therefore, the total number of different words that can be formed using all the letters of the word "ALLAHABAD" is 7560.
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Section I - Solved Mcqs111videos
PERMUTATIONS AND COMBINATIONS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Section II - Assertion Reason Type9videos
PERMUTATIONS AND COMBINATIONS
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PARABOLAEXERCISE - Chapter Test30videos
PARABOLA
- BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - PROBABILITY EXERCISE - Chapter Test45videos
PROBABILITY
Similar Questions
Knowledge Check
- Question 1 - Select One
How many different words can be formed by jumbling the letters in the words MISSISSIPPI in which no two S are adjacent?
A6C4.7C4B6.88C4C6.8.7C4D7.6C4.8C4
The number of different words that can be formed using all the letters of the word 'SHASHANK' such that in any word the vowels are separated by atleast two consonants, is
View SolutionHow many different arrangements can be made by using all the letters in the word MATHEMATICS. How many of them begin with C? How many of them begin with T?
View SolutionHow many seven letters words can be formed by using the letters of the word SUCCESS so that
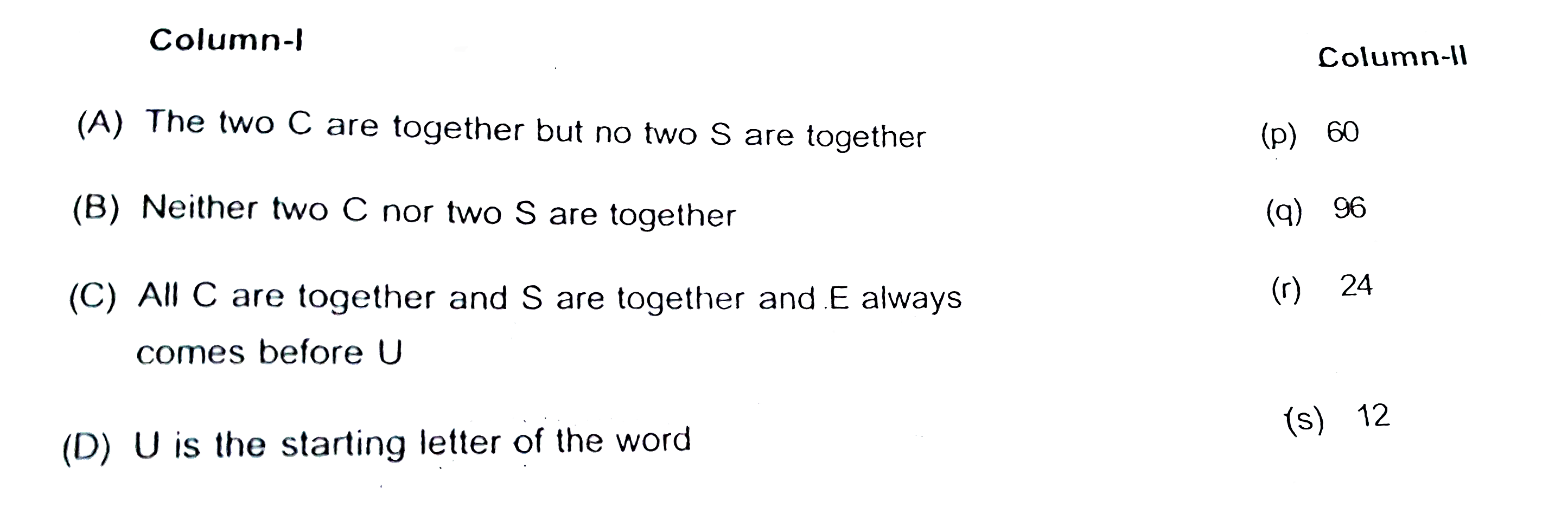 View Solution
View SolutionHow many diferent words can be formed with the letters of the word MATHEMATICS ? In how many of them, vowels are together and consonants are together?
View SolutionHow many three letter words can be made using the letters of the word ORIENTAL?
View SolutionHow many words can be formed using all the letters of the folloiwng words ?
(i) BANANA (ii) ALLAHABAD
INDEPENDENCE (iv) ASSASSINATIONView SolutionHow many different words of 4 letters can be formed with the letters of the word EXAMINATION?
View Solution

