(i) In the given figure, ΔABC is an isosceles triangle in which AB=AC and ∠A=50∘. Find the measure of ∠B and ∠C.

(ii) In the given figure, ΔPQR ia an isosceles triangle in which PQ=PR and ∠Q=70∘. Find ∠P.

Step by step video & image solution for (i) In the given figure, DeltaABC is an isosceles triangle in which AB=AC and /_A=50^(@). Find the measure of /_B and /_C. (ii) In the given figure, DeltaPQR ia an isosceles triangle in which PQ=PR and /_Q=70^(@). Find /_P. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES OF TRIANGLESBOOK - ICSECHAPTER - PROPERTIES OF TRIANGLESEXERCISE - Exercise 18B
10 Videos
- PROPERTIES OF TRIANGLESBOOK - ICSECHAPTER - PROPERTIES OF TRIANGLESEXERCISE - Solved example
16 Videos
- PROFIT AND LOSS BOOK - ICSECHAPTER - PROFIT AND LOSS EXERCISE - EXERCISE 10
18 Videos
- RATIO AND PROPORTIONBOOK - ICSECHAPTER - RATIO AND PROPORTIONEXERCISE - Challenge
1 Videos
Similar Questions
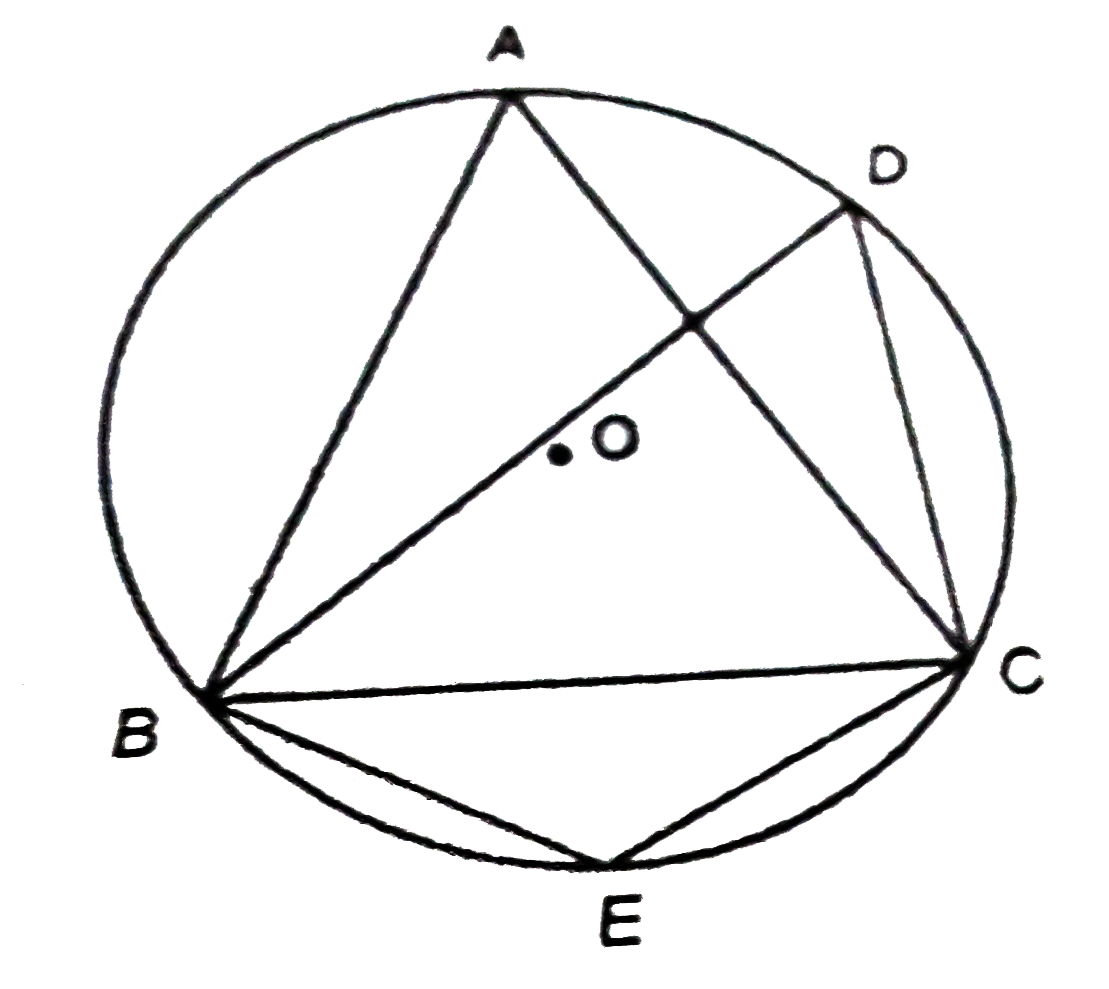
In Figure, ABC is an isosceles triangle with AB=AC and m ∠ABC=500. Find m ∠BDC and ∠BEC
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle. Find the value of ∠BDC and ∠BEC.
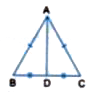
View SolutionIn the adjoining figure, ΔABC is an isosceles triangles in which AB=AC and AD is a median. Prove that :
(i) ΔADB≅ΔADC
(ii) ∠BAD=∠CAD
View SolutionABC is an isosceles triangle with AB = AC = 2a and BC = a . If AD⊥BC, find the length of AD .
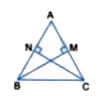
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB=AC. If BM⊥AC and CN⊥AB, prove that :
(i) ΔBMC≅ΔCNB
(ii) BM=CN
View SolutionIn the adjoining figure, ΔABC is an isosceles triangles in which AB=AC and AD is the bisector of ∠A. Prove that :
(i) ΔADB≅ΔADC
(ii) ∠B=∠C
(iii) BD=DC
(iv) AD⊥BC

View SolutionIn the given figure, ΔABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices.
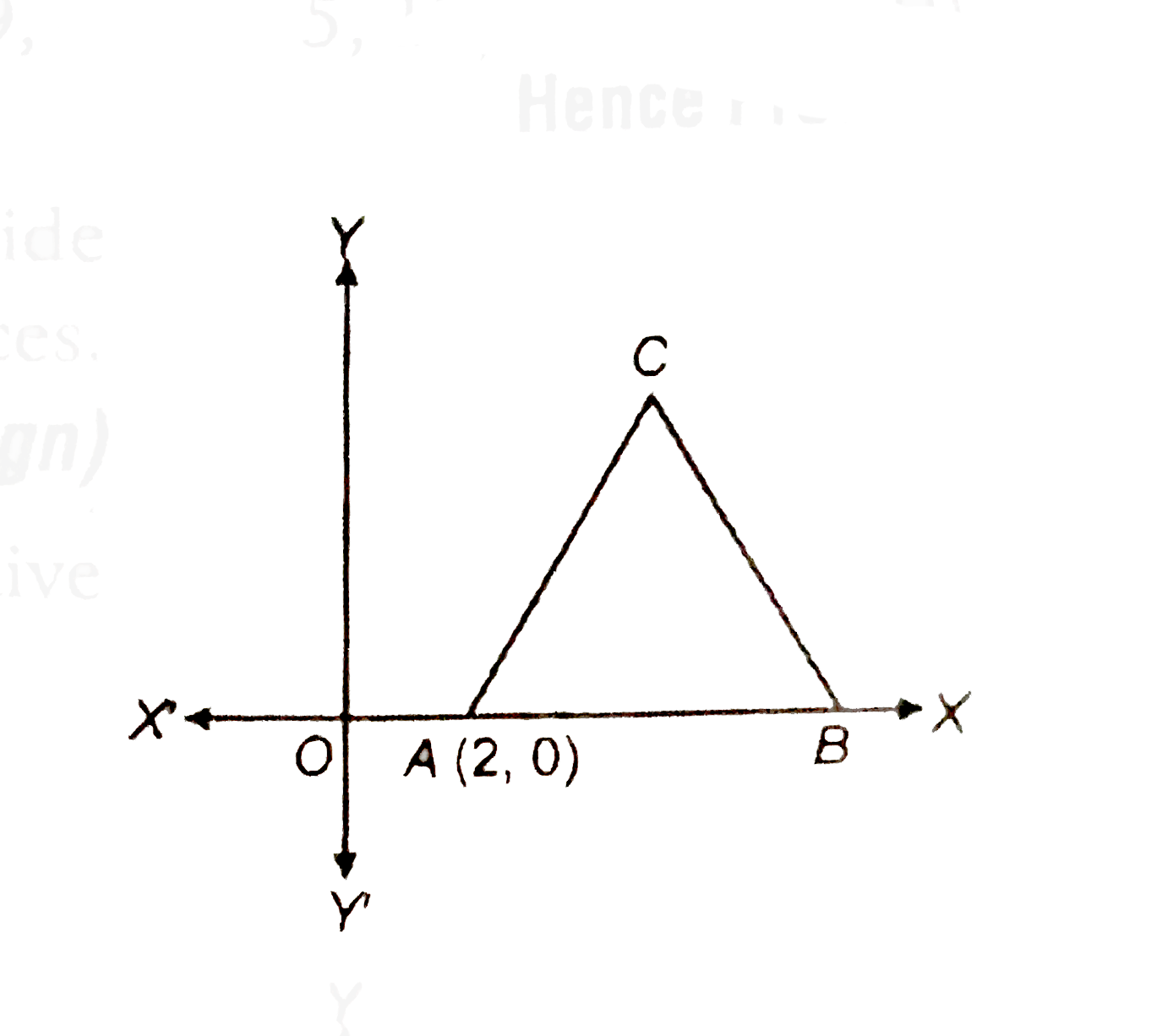
View SolutionIn an isosceles triangle ABC.
AB = BC = 10 cm and BC = 18 cm .
Find the value of :
tan2C−sec2B+2
View SolutionIn an isosceles triangle ABC.
AB = BC = 10 cm and BC = 18 cm .
Find the value of :
sin2B+cos2C
View SolutionIf ΔABC is an isosceles triangle with AB = AC. Prove that the perpendiculars from the vertices B and C to their opposite sides are equal.
View Solution
