If , and , which of the following could be the value of x in degrees (rounded to the nearest degree) ?
63
67
72
77
The correct Answer is:C
To solve the equation tan2x−tanx=6 where 0∘<x<90∘, we will follow these steps:
Step 1: Substitute y=tanx
We start by letting y=tanx. This allows us to rewrite the equation in terms of y:
y2−y=6
Step 2: Rearrange the equation
Next, we rearrange the equation to set it to zero:
y2−y−6=0
Step 3: Factor the quadratic equation
We need to factor the quadratic equation y2−y−6=0. We look for two numbers that multiply to −6 and add to −1. The numbers −3 and 2 fit this requirement:
(y−3)(y+2)=0
Step 4: Solve for y
Now we set each factor to zero:
1. y−3=0 → y=3
2. y+2=0 → y=−2
Step 5: Determine valid solutions for x
Since y=tanx, we have:
1. tanx=3
2. tanx=−2
However, since 0∘<x<90∘, we can only consider the positive solution:
tanx=3
Step 6: Find x
To find x, we take the arctangent:
x=tan−1(3)
Step 7: Calculate x using a calculator
Using a calculator, we find:
x≈71.57∘
Step 8: Round to the nearest degree
Since we need to round to the nearest degree:
x≈72∘
Conclusion
Thus, the value of x in degrees, rounded to the nearest degree, is:
72
---
We start by letting y=tanx. This allows us to rewrite the equation in terms of y:
y2−y=6
Next, we rearrange the equation to set it to zero:
y2−y−6=0
We need to factor the quadratic equation y2−y−6=0. We look for two numbers that multiply to −6 and add to −1. The numbers −3 and 2 fit this requirement:
(y−3)(y+2)=0
Now we set each factor to zero:
1. y−3=0 → y=3
2. y+2=0 → y=−2
Since y=tanx, we have:
1. tanx=3
2. tanx=−2
tanx=3
To find x, we take the arctangent:
x=tan−1(3)
Using a calculator, we find:
x≈71.57∘
Since we need to round to the nearest degree:
x≈72∘
Thus, the value of x in degrees, rounded to the nearest degree, is:
72
Topper's Solved these Questions
Similar Questions
Knowledge Check
If 0∘<x<90∘ and 5sin2x=7sinx−2, what is the vlaue of sin x ?
A1.00B0.71C0.40D0.38If −3<2x+4<9, which of the following CANNOT be a possible value of x?
A−2B−4C0D2If k is a positive constant such that 0<k<1, which of the following could be the graph of y−x=k(x+y) ?
A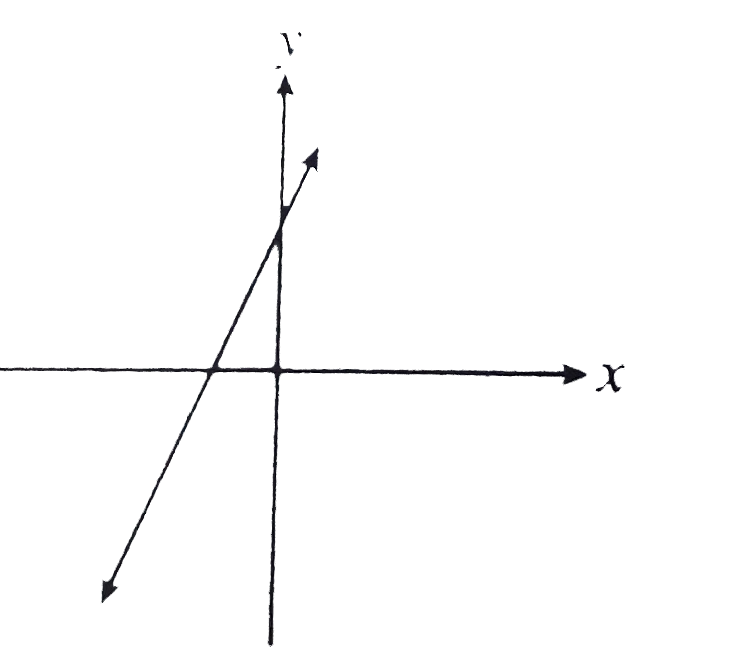 B
B C
C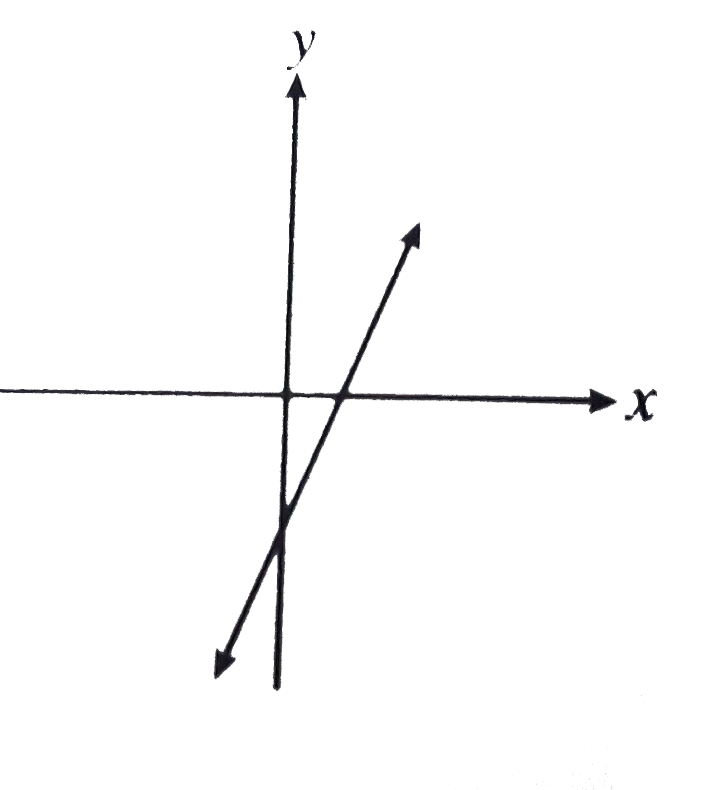 D
D
If 0<x<90∘ and sinx=0.525, what is the value of cos(x3)
View SolutionIf 0<x<π and cosx+sinx=12, then tan x is
View SolutionIf 0<x<π2 and tanx=a2, then cos x =
View SolutionIf (secx)(tanx)<0, which of the following must be true?
I. tanx<0
II. Csc x cot x<0
III. X is in the third or fourth quadrant
View SolutionIf 0<x<π2 and tan 5x = 3 , to the nearest tenth , what is the value of tan x ?
View Solution
