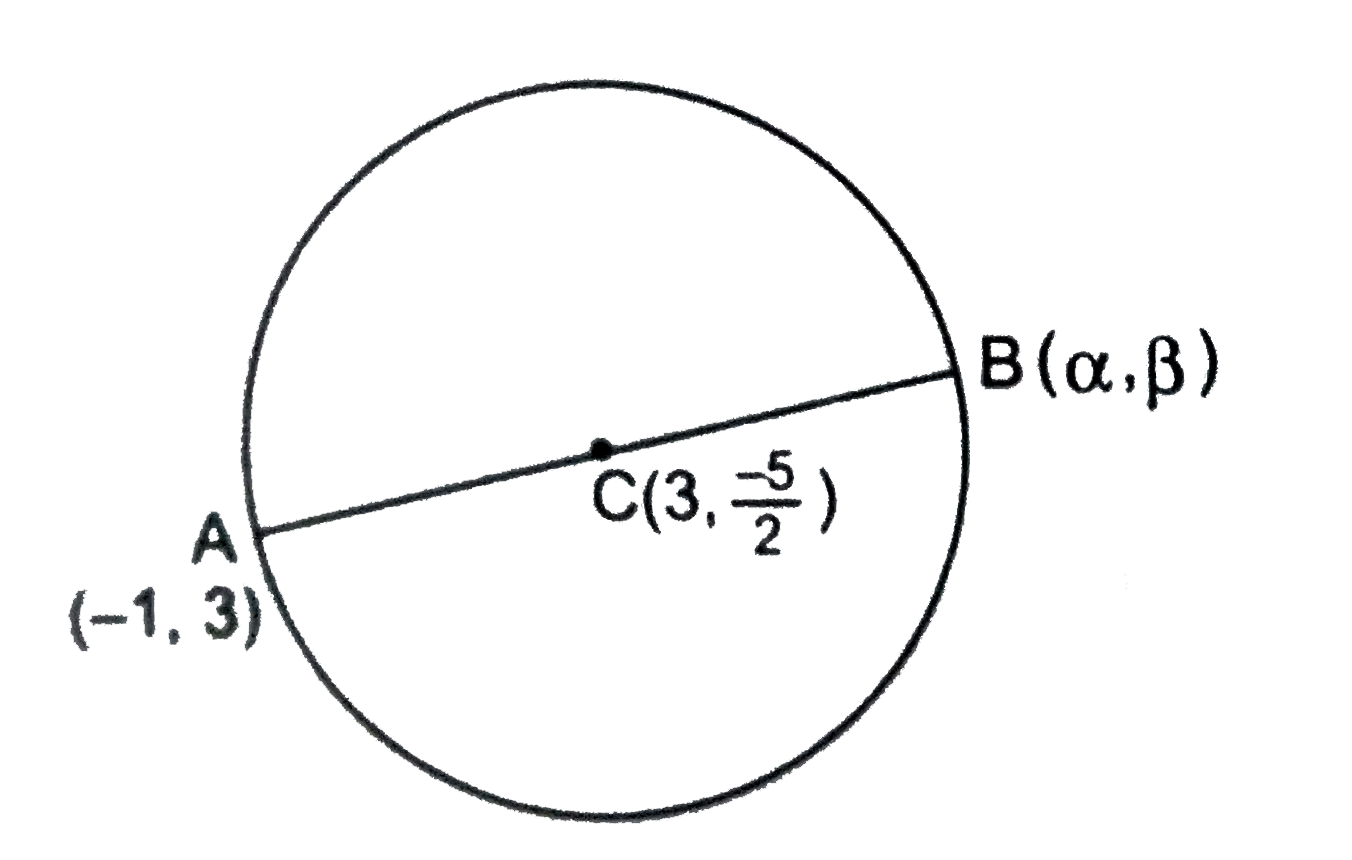
If (−1,3)and(α,β) are the extremities of the diameter of the circle x2+y2−6x+5y−7=0, find the coordinates (α,β).
Video Solution
Text Solution
The correct Answer is:B(7,−8)
Centre of the circle is C(3,−52).
One end of the diameter AB is A(−1,3)
Let the other end of the diameter be B(α,β).
Then, C is the midpoint of AB.
∴(−1+α2=3and3+β2=−52)⇒(α=7andβ=−8).
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If αandβ are the roots of the equation 3x2+7x+3=0 Find the value of αβ:
A1B0C2D3
If α and β are the roots of the equation 4x2−6x+1=0, find the following :
αβ3+α3βView SolutionIf α,β are the roots of 2x2+x+7=0 find the value of α2β+αβ2
View SolutionIf α,β are the roots of 3x2−5x+7=0 then α3+β3=
View Solutionα,β are root of y2−2y−7=0 find α3+β3
View Solutionα,β are root of y2−2y−7=0 find α2+β2
View SolutionIf α and β are the roots of the quadratic equation x2−5x+6=0 then find alpha^2 + beta^2
View SolutionIf αandβ are the zeroes of the polynomial f(x)=5x2−7x+1, then find the value of (αβ+βα).
View Solution

